Homework 1

EECS 376: Foundations of Computer Science

University of Michigan, Winter 2021

Due at 9:00pm, February 3

(grace period through 10:59 pm)

Problems marked with E are graded partially on effort, which means that they are graded in part subjectively on the perceived effort you put into them, rather than solely on correctness. Problems marked with a G are group problems. A group of 1-3 students may work on these together and turn in one assignment for the entire group. Each member listed should have made real contributions. The group problems will be turned in separately on gradescope. For bonus questions, we will not provide any insight during office hours or on Piazza, and we do not guarantee anything about the difficulty of these questions. We strongly encourage you to typeset your solutions in LATEX.

If you collaborated with someone on the non-group problems, you must state their names. You must write your own solution for such problems and may not look at any other student’s write-up.

0. If applicable, state the name(s) and uniqname(s) of your collaborator(s).

1. (a) Use the Euclidean algorithm to compute the GCDs of the following pairs of integers. State how many iterations each one takes to compute, and the value of the potential si at each stage. Verify that indeed 

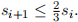
You are encouraged to use a computer for this part.

i. (104, 39)

ii. (710, 140)

iii. (34, 21)

E (b) Try to find pairs of inputs (x, y) such that the number of iterations of Euclid(x, y) is “large”, that is, as close as possible to the upper bound of log3/2(x + y) that we derived in lecture. Can you come up with a hypothesis about what kinds of inputs yield the worst-case running time?

Hint 1: Recall the inequalities used when showing the potential function for the Euclidean algorithm. To minimize the difference between the potential function on steps i and i + 1, what should qi be?

Hint 2: Question 1(a)iii is a worst-case example. Can we apply our choice of qi to derive a relationship between inputs in worst-case examples?

2. (Will this ever end? )

Answer the following questions about potential functions.

(a) Prove that the following mysterious algorithm above terminates on all legal inputs. Don’t worry about what the algorithm is doing...

Input: Non-negative integers x and y which are both less than 188.

1: function Mysterious(x, y)

2:      if x + y = 376 then

3:          return 0

4:       if x = y then

5:          return Mysterious(x + 1, y y 1)

6:       if x > y then

7:          return Mysterious(x, y + 1)

8:       if x < y then

9:          return Mysterious(x + 1, y)

(b) Watch https://www.youtube.com/watch?v=mYAahN1G8Y8 (the card problem from the movie “A Brilliant Young Mind.”) In your own words, explain the problem being solved. Clearly express how a potential function is being used to solve the problem, formulate a potential function in terms of how the problem is stated in the movie, and show it is always decreasing.

3. (A different sort of sort )

The following algorithm computes a topological sort (https://en.wikipedia.org/wiki/Topological_sorting) of a directed acyclic graph. Show that the algorithm always halts.

Input: Directed acyclic graph G = (V, E)

function Kahn-Top-Sort(Directed acyclic graph G = (V, E))

L ← [] // Initialize L to be an empty list

S ← {n ∈ V : n has no incoming edges}

while S is not empty do

S ← S \ {n} for some n ∈ S

L.Append(n)

for each vertex m ∈ V with an edge e = (n, m) ∈ E do

E ← E \ {e}

if m has no incoming edges then

S ← S ∪ {m}

return L

4. In Karatsuba’s Algorithm, each of the two n-bit integers is split into two parts of lengths approximately n/2, and the number of multiplications in each recursion is reduced from 4 to 3. In this question, we will multiply two n-bit integers by splitting each of them into three parts. We will assume for this question that n is an integer power of 3.

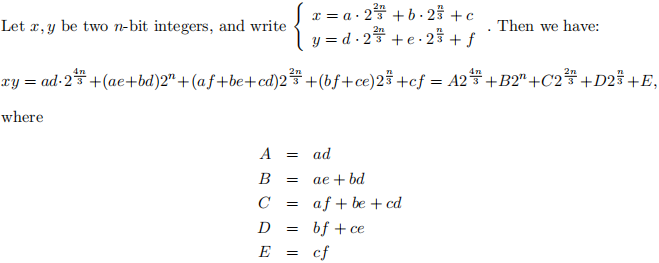
Consider the following two Divide-and-Conquer based algorithms. In Algorithm A, we first compute the values of ad, ae, af, bd, be, bf, cd, ce, cf , recursively. Then, we compute xy by computing A, B, C, D, E based on the equations above. In Algorithm B, we compute A, B, C, D, E by computing Z0, Z1, Z2, Z3, Z4 below, where the multiplication in each of them is computed recursively:

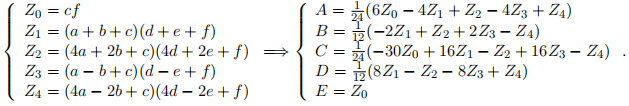
For each algorithm A and B, write down the recurrence relation T(n) for the time complexity, and then compute T(n) explicitly. Which of the algorithms A and B runs asymptotically faster? How do they compare (asymptotically) to Karatsuba’s Algorithm?

Notes:

(i) Dividing an n-bit integer by 3 can be done in O(n) time, if the dividend is known to be a multiple of 3, and you can assume this for this question.

(ii) ln 2 × ln 5 < (ln 3)2 < ln 2 × ln 6

(iii) There is no need to check and/or prove the correctness of the algorithm.

G 5. (Sorting out complaints)

Let n be a power of 2. A group of n students, all of whom have distinct heights, line up in a single-fifile line to get a group picture taken. If a student has any students in front of them who is taller than them, then they will not be seen in the picture. For this reason, every student files one complaint to the photographer for each taller student who is in front of them since each one of these students would individually block the original student from being seen. 

Provide a divide and conquer algorithm using O(n log n) operations which counts the number of complaints which the students will file given an arrangement of the n students.

Hint: The concepts behind Merge Sort may give you some useful ideas here.