Chem113b - Homework assignment 2 2022
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Chem113b - Homework assignment 2
2022
(I) As we will learn later, the wavefunction of the 1s electron in a Hydrogen atom is αe −r/a0 , where a0 is the Bohr radius corresponding to 0.529177A˚(we will “discover” it later) and α is the normalization constant. Express α in terms of a0 and find the value of it.
[Hints: The probability of normalized wavefunction over all space is 1. Use Jacobian de- terminant for the whole space integral. When doing the integration by parts, note that for
exponential function f(x) = ex , fdx = df.]
(II) Consider these operators:
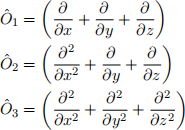
acting on these wave functions:
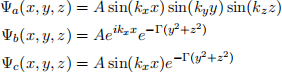
Assume that Γ ∈ R and Γ > 0. Act with each operator on each wavefunction and based on the result, decide if the given wavefunction represents an eigenstate of the operator? If so, what is the eigenvalue? Provide a detailed answer and show your reasoning mathematically.
(III) Consider matrices A and B:

One of them is Hermitian, i.e., it is qual to its conjugate transpose. Which one is it? Hermitian matrices yield real eigenvalues, while the eigenvalues of the non-Hemitian matrices can have imaginary component. Compute the eigenvalues ({λ}) of A and B, using the characteristic polynomial; for A it is:
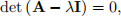
where I is an identity matrix. Do your findings confirm the previous statement on Hermitian matrices? Provide full solution and a detailed answer.
In Quantum mechanics, operators are often represented in a matrix form. Consider a wave function that is an eigenvector of an operator. Is it important for an operator to be represented by a Hermitian matrix, why? Provide detailed reasoning.
(IV) The Heisenberg uncertainty principle provides the lower bound for the uncertainty in some
pairs of observables (so-called canonically conjugate variables). Let’s see it in practice:
A: The uncertainty of speed is measured for an electron, H atom, and a steel ball of mass 2.5 kg. In both cases the precision determines the velocity with precission of 10 −3 m s − 1. What is the uncertainty in position for all three objects? Based on these results, explain why we can neglect the uncertainty in classical mechanics, i.e., for macroscopic objects.
B: Consider an excited atom of Na, which loses energy by radiating a photon (and hence
it stabilizes in its ground state). During this process the atom emits radiation at the wavelength of λ = 528.7 nm. The lifetime τ of this excited state is 24.8ns, what is the uncertainty in energy of this excited state? When you consider a measured spectrum, will the peak at λ = 528.7 nm be a sharp line? Provide a detailed answer.
(V) Assume a wave function for an electron in one dimension has a Gaussian formula Ψ(x) = αe −βx2 where β = 3.14A˚ −2 .
A: Sketch the wavefunction, find the normalization constant α. Find the most probable
position of an electron and the mean position to find an electron; indicate them in your plot. Use the expectation value integral to compute ⟨x⟩, but you do not have to perform any integration to rationalize your result.
Hint: the Gaussian integral is
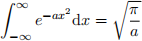
B: Determine the uncertainty in the position.
Hint: use the expression for normal distribution - you do not have to use any complicated calculation.
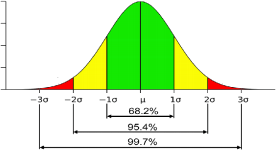
C: The figure below, which depicts a Gaussian distribution and the integral value around
its mean (denoted µ). The percentage tells you what portion of the distribution is found around the mean value in a given interval, e.g., 99.7% of the statistical observations fall within the range of three times of the standard deviation σ (denoted ±3σ) around the mean. Estimate the probability to find an electron at a distance < 0.564A˚ away from the mean position of the electron ⟨x⟩ .
D: Check that the Heisenberg uncertainty is satisfied for the position and momentum. You
need to compute the expectation value of the momentum operator pˆx and its square. The uncertainty for an operator Oˆ is simply 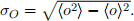 You will find that the Gaussian wave function satisfies the uncertainty relation at the lowest possible bound.
You will find that the Gaussian wave function satisfies the uncertainty relation at the lowest possible bound.
Hint: solve the problem generally (i.e., without plugging in the values of α and β) and you will see that the result is general (i.e., independent of the particular value of α and β).
(VI) Consider a particle in a 1D infinite potential well of size L, i.e., the potential is:
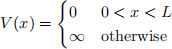
The particle is thus confined to x ∈ (0,L). Assume that the quantum particle is in a state with (a rather weird) wavefunction:
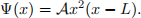
It is easy to see that this function (correctly) vanishes at the boundaries.
A: The factor A guarantees proper normalization; what is its value?
B: What is the probability to find a particle in the region 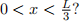
2022-02-08