Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

AMATH 301

Homework 6: Autumn 2021

Consider Fourier mode expansions on the domain x ∈ [0, 2π] (divide the domain into 200 points) which take the following forms:

(a) Construct the sine basis ψn = cnsin(nx/2) where cn is a normalization constant in order to make an orthonormal basis. Specifically, construct a matrix A1 with 10 columns (and 200 rows) of orthonormal vectors corresponding to n = 1, 2,．．．10.  Compute the correlation matrix A2=A1T A1.  (check to see that A2 looks like the identity).

ANSWER: Should be written out as matrices A1 and A2 respectively.

(b) Construct the cosine basis φn = cncos(nx/2) where cn  is a normalization constant in order to make an orthonormal basis. Specifically, construct a matrix A3 with 10 columns (and 200 rows) of orthonor- mal vectors corresponding to n = 0, 2,．．．9. Compute the correlation matrix A4=A3T A3 (check to see that A4 looks like the identity).

ANSWER: Should be written out as matrices A3 and A4 respectively.

(c) Compute the correlation matrix between the sine and cosine basis A5=A1T A3 (check to see that A5 does not look like the identity).

ANSWER: Should be written out as matrix A5.

(d) Using the sine basis A1, approximate the function f (x) = cos(x).  Specifically, compute the norm of the error between the function and your approximation

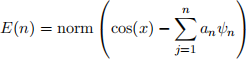
for n = 1, 2,．．．n. Note that the ψn  are the columns of A1. So you just need to compute the projection

of each mode onto the function f (x), i.e. the an  is the dot product of f (x) with ψn . ANSWER: Save the 1 by 10 vector E as A6.