Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAT150A – Modern Algebra – Fall 2021

Homework Three

1. Consider Q and Z as additive groups. Let G = Q/Z.

(i) Describe the elements of G.

(ii) Show that every element of G has finite order.

(iii) Is G a finite group? Justify your answer.

2. Determine if O2(R) is a normal subgroup of GL2(R).

3. Let O2(R) be the orthogonal group. Let f, g, h ∈ O2(R) such that f and g are reflections, and h is a rotation.

(i) Prove that fg is a rotation.

(ii) Prove that fh is a reflection.

(iii) Show that O2(R) contains an element of order n for every n ∈ N.

(iv) Show that O2(R) contains infinitely many elements of order 2.

4. (i) Prove that rtv = tur in E2, where u = r(v) and r is reflection in the e1-axis.

(ii) Prove that ρθtv = twρθ in E2, where w = ρθ(v), and ρθ ∈ SO2(R).

(iii) Let

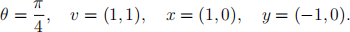
Illustrate the relation in (ii) by drawing what happens when the isometries f = ρθtv and g = twρθ are applied to the points x, y ∈ R².

(iv) Find the fixed point of the isometry f = ρθtv when and v = (1, 1).

5. Let f ∈ E2 be a glide reflection. Prove that f²  is a translation.

6. (i) Sketch the lattice Z(2, 0) + Z(1, 3).

(ii) Sketch the lattice Z(1, ) + Z(−1, ).

(iii) Sketch the lattice Z(3, 0) + Z(4, 1).

In each case plot at least 20 points.

7. (i) Let

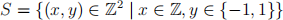
be a frieze pattern in R², and let G be the associated frieze group. Find the translation subgroup of G, and the point group of G.

(ii) Let

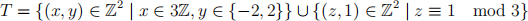
be a frieze pattern in R², and let H be the associated frieze group. Find the translation subgroup of H, and the point group of H.

(iii) Let

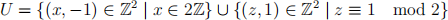
be a frieze pattern in R², and let J be the associated frieze group. Find the translation subgroup of J, and the point group of J.

(iv) Plot the patterns S, T, and U on different axes, and indicate the reflections, glide reflections, and rotations in their symmetry groups.

8. (i) Look around your home or neighborhood for something which has two in-dependent directions of discrete translational symmetry. Take a photo of the pattern that you find. For example, it could be a piece of fabric, or kitchen or bathroom tiles, or carpet, or wallpaper, or a fence.

(ii) On the photo, mark the lattice.

(iii) On the photo, indicate all rotations, reflections, and glide reflections. If there are rotations, what are their orders?

(iv) Compare your pattern with the wallpaper patterns on p174 of Artin (also posted on Canvas). Which one has the same wallpaper group as your pat-tern?

(v) Repeat parts (i)–(iv) with a second pattern. Make sure it corresponds to a different wallpaper group than your first pattern.

9. Let X = {1, 2, 3, 4} and let the symmetric group S4 act on X by permutations.

(i) What is the orbit of 1 under this action?

(ii) What is the stabilizer of 1 under this action?

(iii) Verify that the orbit-stabilizer theorem holds for this action.