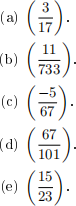Math 3527 Number Theory 1, Spring 2024 Homework 10
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Math 3527 Number Theory 1, Spring 2024 Homework 10, due Fri Apr 12th.
Part I: No justi cations are required for these problems. Answers will be graded on correctness.
1. For each integer, determine whether it can be written as a sum of two squares (of integers), and for those that can, give at least one such way:
(a) The integer 2600.
(b) The integer 2020.
(c) The integer 2024.
(d) The integer 77077.
(e) The prime 2909, given that 8782 三 — 1 (mod 2909).
(f) The prime 5813, given that 7962 三 — 1 (mod 5813).
2. The goal of this problem is to nd some of the 20 Pythagorean right triangles with one side of length 2024 = 23 · 11 · 23.
(a) Find the four Pythagorean triangles having one leg of length 2024, and whose side lengths are relatively prime. [Hint: Find the possible pairs (s; t) with 2st = 2024 where s > t and s; t have opposite parity.]
(b) Find the four Pythagorean triangles having one leg of length 2024, and whose side lengths have greatest common divisor 2.
(c) Find the two Pythagorean triangles having one leg of length 2024, and whose side lengths have greatest common divisor 8. [Hint: Factor s2 — t2 as (s — t)(s + t).]
(d) Explain brie y why there are no Pythagorean right triangles with a hypotenuse of length 2024.
3. List all of the (nonzero) quadratic residues, and all of the quadratic nonresidues, modulo 13 and modulo 19.
4. Calculate the following Legendre symbols (i) using Euler's criterion, and (ii) using quadratic reciprocity.
(f) Which method is easier to implement by hand?
Part II: Solve the following problems. Justify all answers with rigorous, clear explanations.
5. Prove that if an integer is the sum of squares of two rational numbers, then it is the sum of squares of two integers: for example, 5 = (22/13)2 + (19/13)2 = 22 + 12 . [Hint: Clear denominators and use the characterization of sums of two squares.]
6. The goal of this problem is to discuss some results on consecutive integers that are sums of two squares.
(a) If N is the sum of two squares, show that N must be congruent to 0, 1, 2, 4, or 5 modulo 8.
(b) Deduce that there do not exist four consecutive integers all of which are the sum of two squares.
(c) Show that there exist in nitely many N for which N , N + 1, N + 2 are all the sum of two squares. [Hint: Try N = 4a4 + 4a2.]
7. Recall (cf. Homework 1) that the Fibonacci numbers Fn are de ned by F1 = F2 = 1 and Fn+1 = Fn + Fn- 1 for n ≥ 1. The goal of this problem is to show that if Fk isa prime congruent to 1 modulo 4, then (i) Fk is the sum of two squares of Fibonacci numbers and (ii) the two square roots of -1 modulo Fk are also Fibonacci numbers.
(a) Verify the results for the Fibonacci primes F5 = 5, F7 = 13, and F11 = 89.
(b) Suppose Fk is prime and k > 4. Show that k must be odd. [Hint: Use an identity from problem 4(c) of homework 1.]
(c) Suppose that Fk is a prime congruent to 1 modulo 4: then Fk can be written uniquely as the sum of two squares Fk = a2 + b2 for positive a,b. Show that both a and b are Fibonacci numbers. [Hint: Use the other identity from problem 4(c) of homework 1.]
(d) Prove that Fn(2)+1 - Fn Fn+2 = (-1)n for all positive integers n.
(e) Suppose that Fk is a prime congruent to 1 modulo 4: then -1 is a square modulo Fk . Show that the two square roots of -1 modulo Fk are Fk- 1 and Fk-2. [Hint: Use (d).]
8. Let p be a prime.
(a) If p ≠ 2, 3, show that at least one of 2, 3, and 6 is a quadratic residue modulo p.
(b) Show that the polynomial q(x) = (x2 - 2)(x2 - 3)(x2 - 6) has a root modulo p for every prime p, but has no integer roots.
2024-04-13