STA 130B Homework 1 Spring 2024
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Homework 1
STA 130B | A. Farris | Spring 2024
A pdf copy of your homework solutions is due at 5pm on Thursday, April 11. Submission of the pdf will be through Gradescope. You must write up and turn in your own solutions, but if you do work on them with some of your classmates, list their names as collaborators on your submission. You must explain your answers for full credit.
Problems
1. Suppose that X has a Binomial(n, p) distribution, where 0 < p < 1. Define 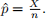
(a) What is the support of the random variable
?
(b) What are the expected value and variance of
?
(c) What is the expected value of
(1 −
)?
(d) If p ≈ 0, is
typically more likely to be higher or lower than its expected value?
(e) If p ≈ 1, is
typically more likely to be higher or lower than its expected value?
(f) If p ≈ 0 or p ≈ 1, is
(1 −
) typically more likely to be higher or lower than its expected value?
(g) When
(1 −
) is smaller than its expected value, the quantity
is typically also smaller than expected. When this occurs, the (random) Wald confidence interval
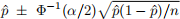
for the unknown proportion p tends to be smaller than it ought to be; and, as a consequence, the coverage probability of this interval is lower than desired value of 1 − α. Similarly, if
(1 −
) is larger than expected, this confidence interval tends to be larger than it ought to be; and, therefore, the coverage probability tends to be higher.
So: if p ≈ 0 or p ≈ 1, does the Wald confidence interval tend to have a probability of coverage that is too high, or too low?
2. Let X represent the number of days that transpire until the next accident at a workplace. Assume that X has a Geometric(0.2) distribution.
(a) Starting on day 0, what is the probability that the next accident occurs on the following day (i.e. what is P(X = 1))?
(b) What is the probability that the next accident hasn’t happened yet after the first week (i.e. what is P(X > 7))?
(c) If the next accident hasn’t happened yet after the first week, what is the probability that it occurs on the following day? (i.e. what is P(X = 8|X > 7))?
(d) If the next accident hasn’t happened yet after the first week, what is the probability that it hasn’t happened yet after the following week, either?
3. The number of 911 calls in a city over the course of one night, Z, can be broken into the number of calls regarding a medical emergency (X) and the number of other calls (Y ).
To model this, suppose that X ∼ Poisson(µ) and that Y ∼ Poisson(ν) for some µ, ν > 0, and that X and Y are independent. It follows from this that Z = X + Y has a Poisson(µ + ν) distribution. Let’s define 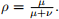
What is the conditional probability of X = x given that Z = n for integers 0 < x < n? Write your answer in terms of n, ρ, and x.
4. Suppose that, for some 0 ≤ p ≤ 1, U and V are two random variables with joint PMF
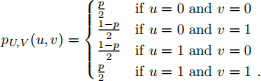
(a) What is the marginal distribution of U?
(b) What is the marginal distribution of V?
(c) What is the conditional distribution of V given U = 1? Are U and V independent?
(d) What is the distribution of U + V?
(e) What is P(U = V )?
(f) For what value of p would it be fair to say that U = 1 − V?
(g) Do the marginal distributions for any two random variables determine their joint distribution? Explain.
5. Let X have CDF FX(x) = x 5 for 0 < x < 1.
(a) What is P(X > 0.4)?
(b) What is the expected value of X?
6. Suppose that X has PDF fX(x) = c (x 2 + 2x + 1) I[−1,1](x).
(a) What is P(X ≥ 0)?
(b) What is the CDF of this distribution?
(c) What is E(X)?
2024-04-12