COMP 360 Winter 2022 Assignment 5
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP 360 Winter 2022
Assignment 5
Due: Friday, April 8th, 11:59pm
Please submit the assignment on Crowdmark by the due date. In all problems below where you are asked to give an efficient algorithm, you must also prove that your algorithm is correct and analyze its running time. If you use any sources other than the course textbook or the lecture notes (e.g. other textbooks, online notes, friends) please cite them for your own safety. Do not upload this assignment to any online repository. Also, a reminder that direct copying from sources is not permitted, and solutions must be in your own words.
Questionsc
1. A k-star is the graph on k + 1 vertices u, v1 , v2 , . . . , vk with edgesuv i for each i ∈ [k]. A graph G = (V, E) is k-star free if it does not contain a k-star: so, if we look at any subset of k + 1
vertices U ⊆ V in G, the subgraph of G on the vertices in U is not a k-star. [10]
(a) For each positive integer k ≥ 3, give an example of a graph G k = (Vk, Ek) that is k-star free but has a vertex with degree greater thank.
(b) Consider the following weighted version of the Independent Set problem. The input is a graph G = (V, E) with a non-negative integer vertex weight w(u) ≥ 0 for each u ∈ V. The goal is to find an independent set U ⊆ V in G such that w(U) :=Σu∈U w(u) is maximized. For any k ≥ 3, give a polynomial-time k-approximation algorithm for the Weighted Inde-
pendent Set problem on k-star free graphs. (Hint: Use the obvious greedy algorithm!)
2. Consider the Max SAT problem. As input, you receive a CNF formula F = C1 ∧ C2 ∧ · · · ∧ Cm on n variables. The goal is to find a boolean assignment x ∈ {0, 1}n which satisfies as many clauses as possible.
Prove that the following is a 2-approximation algorithm for the Max SAT problem. Given F, output the all-1s assignment or the all-0s assignment, whichever satisfies more clauses. [10]
3. Updated on April 1st. Consider the following variation of the Weighted Vertex Cover problem. As input you receive a graph G = (V, E) with vertex weights w(u) ≥ 0 for all u ∈ V. The goal is to find a subset of vertices U ⊆ V such that [10]
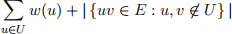
is minimized. In other words, the set U does not have to be a vertex cover: it can leave some edges uncovered, but must pay for each uncovered edge.
(a) Create an integer program that solves the above variant of the Weighted Vertex Cover problem exactly. Your integer program should have a variable xu ∈ {0, 1} for every vertex u ∈ U and a variable ye ∈ {0, 1} for every edge e ∈ E.
(b) Now, find a polynomial-time 3-approximation algorithm for this problem by rounding a solution of the linear programming relaxation of your integer program from part (a).
4. Let k > 0 be any positive integer, and consider the following restricted version of the Set Cover
problem. As input you receive a positive integer n and sets S1, S2 , . . . , Sm ⊆ [n] such that for all i ∈ [n], i appears in at most k of the given sets. The goal is to choose I ⊆ [m] such that "i∈ISi = [n] and |I| is minimized.
Give a polynomial-time k-approximation algorithm for this restriction of the Set Cover problem. [10]
5. Consider the following modification of the Center Selection problem. As input, you receive a list of points p1 , p2 , . . . , pn ∈ [0, 1]2 with rational coordinates in the plane. Note that each point is contained within the unit square [0, 1]2 , and the distance between any two pairs of points is the usual Euclidean distance [15]
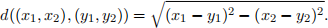
The goal is to find the minimum r ≥ 0 such that we can cover all the given points with 3 circles of radius r.
In this question we develop a PTAS for this problem. So, we give an algorithm which, for any ε > 0, runs in time polynomial inn that outputs a solution with approximation factor (1 + ε).
(a) Suppose the optimal radius is r∗ , and let c1 , c2 , c3 be the centers of circles covering all points in the input, each with radius r∗ . Divide the unit square [0, 1]2 into a grid of square cells each of which has side-length r∗ε/2. Argue that there exists a set of three points c![]() , c
, c![]() , c
, c![]() on this grid such that circles of radius (1 + ε)r∗ centered at c
on this grid such that circles of radius (1 + ε)r∗ centered at c![]() , c
, c![]() , c
, c![]() cover all points in the input.
cover all points in the input.
(b) We can get an approximation of r∗ even if we cannot compute it exactly. Use the Center Selection algorithm to get a 2-approximation to this problem.
(c) Modify the argument from part (a) and combine it with part (b) to obtain a PTAS for this problem.
2024-01-20