COMP 360 Winter 2022 Assignment 3
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP 360 Winter 2022
Assignment 3
Due: Saturday, February 26th, 11:59pm
Please submit the assignment on Crowdmark by the due date. In all problems below where you are asked to give an efficient algorithm, you must also prove that your algorithm is correct and analyze its running time. If you use any sources other than the course textbook or the lecture notes (e.g. other textbooks, online notes, friends) please cite them for your own safety. Do not upload this assignment to any online repository. Also, a reminder that direct copying from sources is not permitted, and solutions must be in your own words.
Questions
1. Let G = (V, E) be a graph. Recall a vertex cover is a subset of vertices U ⊆ V such that for every e ∈ E at least one endpoint of e is in U. Consider the following linear program, which intuitively encodes (a fractional relaxation of) the “Minimum Vertex Cover” problem. [10]
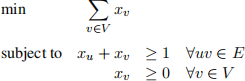
(a) For each integer k ≥ 3, construct a graph Gk such that the size of the smallest vertex cover on Gk is k − 1, but there is a solution x* to the above LP such that 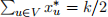 . (This shows that a “fractional” Vertex Cover can be smaller than a real Vertex Cover).
. (This shows that a “fractional” Vertex Cover can be smaller than a real Vertex Cover).
(b) Construct the dual to this linear program. What problem does the dual solve?
(c) Let G = (V, E) be a bipartite graph. Here is nice fact: if G is bipartite, then the optimal value of the above linear program is actually equal to the size of the minimum vertex cover on G. (This is a surprise, in light of (a)!)
Let G be bipartite, let M ⊆ E be a maximum matching on G, and let U ⊆ V be a minimum vertex cover on G.
• Prove that for any vertex u ∈ V , if u is not matched in M then u 6
U.
• Prove that for any edge uv ∈ E, if both u, v ∈ U, then uv 6
M.
2. Consider the following problem. As input, you receive an undirected graph G = (V, E) and two non-negative integers k, 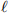 ≥ 0. The goal is to decide if it is possible to delete at most k vertices from G (along with their neighbouring edges) so that the remaining graph has an independent set of size at least
≥ 0. The goal is to decide if it is possible to delete at most k vertices from G (along with their neighbouring edges) so that the remaining graph has an independent set of size at least 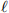 . [5]
. [5]
Prove that this problem is NP-Complete.
3. In class we considered the (Exact) k-SAT problem, where you are given a CNF formula F such that each clause has k literals and want to determine if F is satisfiable. In this problem, we consider the (≥ k)-SAT problem, where you are given a CNF formula F such that each clause has at least k literals and want to determine if F is satisfiable. [10]
(a) Prove that the (≥ n)-SAT problem is in P, where n is the number of input variables in the boolean formula.
(b) Prove that the (≥ log n)-SAT problem is NP-Complete, where n is the number of input variables in the boolean formula.
4. You’re planning an awesome party in order to become friends with all the cool kids. However, [10] your house can only fit a small number of people, and, because of this, you won’t be able to invite all the cool kids. Instead, you hatch a plot: you will (through intensive research) figure out the entire social network of cool kids (that is, who is friends with whom), so that you can invite a small subset S of the cool kids who, together, are friends with all the cool kids. That way, when you invite the kids from the set S, all the cool kids will eventually find out about the amazing party you threw.
Unfortunately, on further thought, you realize that this problem is NP-Complete. Here is a formalization of it. As input, you are given a set of kids K, along with the knowledge, for each distinct a, b ∈ K, whether or not a and b are friends. You are also given a positive integer k. The goal is to find a subset of kids S ⊆ K such that |S| ≤ k and every kid in K is friends with some kid in S. Prove that this problem is NP-Complete.
5. Consider the following modification of the independent set problem. As input, you receive an undirected graph G = (V, E). As output, you must decide if G contains an independent set U ⊆ V such that U contains at least 99% of the vertices in V (that is, |U| ≥ 0.99|V |). [10]
Prove that this modification of the independent set problem is NP-Complete.
2024-01-10