Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Department of Mathematics and Statistics

MATH 324: Statistics

Fall 2023

Assignment 1

Q1.  Suppose that Y1  , Y2  , . . . , Yn  constitute a random sample from a population with probability density function

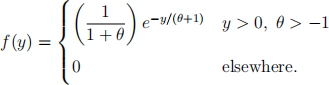
Suggest a suitable statistic to use as an unbiased estimator for θ .

Hint: Consider Y.

Q2.  The number of breakdowns per week for a type of minicomputer is a random variable Y with a Poisson distribution and mean λ. A random sample Y1  , Y2  , .  .  .  , Yn  of

observations on the weekly number of breakdowns is available.

a.  Suggest an unbiased estimator for λ .

b. The weekly cost of repairing these breakdowns is C = 3Y + Y2 .  Show that E(C) = 4λ + λ2 .

c.  Find a function of Y1 , Y2 ,  .  .  .  , Yn  that is an unbiased estimator of E(C).

[Hint: Use what you know about Y and (Y)2  .]

Q3. We have seen that if Y has a binomial distribution with parameters n and p, then Y/n is an unbiased estimator of p. To estimate the variance of Y , we generally use n(Y/n)(1 - Y/n).

a.  Show that the suggested estimator is a biased estimator of V (Y).

b. Modify n(Y/n)(1 - Y/n) slightly to form an unbiased estimator of V (Y).

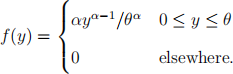
where α > 0 is a known, ixed value, but θ is unknown.  Consider the estimator θˆ =max(Y1 , Y2 , .  .  .  , Yn ).

a.  Show that θˆ is a biased estimator for θ .

b. Find a multiple ofθˆ that is an unbiased estimator of θ .

c. Derive MSE(θˆ).

Q5. If Y has a binomial distribution with parameters n and p, then ˆ(p)1   = Y/n is an

unbiased estimator of p. Another estimator of p is ˆ(p)2  = (Y + 1)/(n + 2).

a.  Derive the bias ofˆ(p)2 .

b. Derive MSE(ˆ(p)1 ) and MSE(ˆ(p)2 ).

c. For what values of p is MSE(ˆ(p)1 ) < MSE(ˆ(p)2 )?

Q6.  Suppose that E(θ(ˆ)1 ) = E(θ(ˆ)2 ) = θ , Var(θ(ˆ)1 ) = σ 1(2), and Var(θ(ˆ)2 ) = σ2(2) ,.  Consider the estimator θ(ˆ)3  = aθ(ˆ)1  + (1 - a)θ(ˆ)2 .

a.  Show that θ(ˆ)3  is an unbiased estimator for θ .

b.  If θ(ˆ)1  and θ(ˆ)2  are independent, how should the constant a be chosen in order to minimize the variance ofθ(ˆ)3 ?

c.  How should the constant a be chosen to minimize the variance of θ(ˆ)3  if θ(ˆ)1   and θ(ˆ)2  are not independent but are such that Cov(θ(ˆ)1 , θ(ˆ)2 ) = c 0?