Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

COMP9020

Sample exam

2022 Term 3

Problem 1

Prove or disprove the following:

(a) For all x, y, z ∈ N: If x|z and y|z then (x + y)|z

(b) For all x, y, z ∈ N>0: If x =(z) y and y =(x) z then z =(y) x

Problem 2

Define f : Z → Z as f(n) = (n div 8) + (n % 8)

Prove that 7|n if and only if 7| f(n)

Problem 3

Prove, or provide a counterexample to disprove:

(a) For all sets A, B: B ∩ (A ∪ (B ∩ Ac )) = B ∪ (A ∩ (B ∪ Ac ))

(b) For all sets A, B, C, D: (A × B) ∪ (C × D) = (A ∪ C) × (B ∪ D)

Problem 4

Order the following functions in increasing order of asymptotic complexity:

• n √log n

• √n 2 log n + 2n 3

• √n(log n)

• T(n) where T(n) = 3T(n/2) + 2n; T(1) = 1

• T(n) where T(n) = T(n − 1) + log n; T(1) = 1

• T(n) where T(n) = 3T(n/3) + 2n log n; T(1) = 1

Problem 5

Let R ⊆ A × A be a partial order and let f : B → A be an arbitrary function.

Define S ⊆ B × B as follows:

(x, y) ∈ S if and only if (f(x), f(y)) ∈ R

Prove or disprove the following:

(a) If f is surjective then S is a partial order

(b) If f is injective then S is a partial order

Problem 6

Prove or disprove the following:

For all graphs G and H where H is a subdivision of G:

(a) The clique number of H is less than or equal to the clique number of G

(b) The chromatic number of H is less than or equal to the chromatic number of H.

Problem 7

Give, with justification, an example of an undirected graph with 6 vertices, 9 edges which is regular and planar.

Problem 8

For each of the following code snippets, provide an asymptotic upper bound for T(n), the running time of the code.

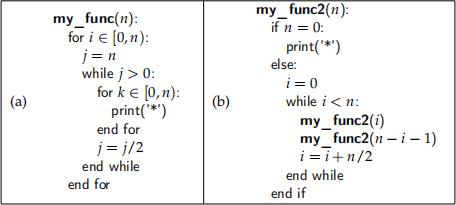
Problem 9

Let Σ = {a, b} and define L ⊆ Σ* recursively as follows:

• λ ∈ L

• If w ∈ L then awb ∈ L

• If w1, w2 ∈ L then w1w2 ∈ L

a Which of the following words are in L:

• aabb

• abab

• abba

• baab

b Let P(w) be the proposition that w has the same number of a’s as b’s. Prove that P(w) holds for all w ∈ L.

Problem 10

Let PF be the set of all propositional formulas.

Define f : PF → Pow(PF) by

f(ϕ) = {ψ ∈ PF : ϕ |= ψ}

Prove or disprove the following:

(a) For all ϕ, ψ ∈ PF: f((ϕ ∧ ψ)) = f(ϕ) ∩ f(ψ)

(b) For all ϕ ∈ PF: f(¬ϕ) = (f(ϕ))c

Problem 11

Let f : B4 → B be the boolean function defined as:

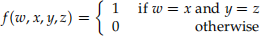
Which of the following boolean functions are equal to f ?

(i) ((w&&x) || (y&&z)) || ((!w&&!x) || (!y&&!z))

(ii) ((1+w + x) · (1+y + z))%2

(iii) 1 − ((w + x) · (y + z)%2)

(iv) ((w||x) && (y||z)) && ((!w||!x) && (!y||!z))

(v) max{|1 − (w + x)|, |1 − (y + z)|}

(vi) min{1 − |w − x|, 1 − |y − z|}

Problem 12

Consider the following timetabling arrangement given in lectures:

The school administrator would like to know if it is possible to arrange an exam schedule where 3 (or more) subjects can be examined at the same time without any student having a clash (i.e. two or more exams at the same time)

Do ONE of the following:

• Explain how this can be modelled as a graph theory problem, OR

• Explain how this can be modelled as a propositional logic problem.

In particular:

• Explain how to define a suitable graph OR an appropriate set of propositional variables and formulas to model the situation

• Describe the associated graph theory / logic problem that needs to be solved

• Indicate how you could solve the problem. You do not have to find a solution

Problem 13

We would like to pave a 1 × n rectangular path with a mix of 1 × 1 and 1 × 3 paving stones.

For example, if s represents a 1 × 1 stone and t represents a 1 × 3 stone, then possible ways of tiling a 1 × 6 path include:

• ssssss

• tt

• ssst

• ssts

• tsss

(Note that direction matters: e.g. ssst and tsss should be considered different arrangements)

a Let P(n, k) be the number of different arrangements of paving stones that can pave a 1 × n path using exactly k 1 × 3 paving stones.

Express P(n, k) either:

• in terms of combinatorial functions defined in lectures; or

• recursively (including base cases) in terms of P(n 0 , k 0 ) where n 0 ≤ n and k 0 ≤ k.

b Let P(n) = P(n, 0) + P(n, 1) + . . . be the number of arrangements of paving stones that can pave a 1 × n rectangular path.

Find a recurrence equation for P(n) and provide, with justification, an asymptotic upper bound.

Problem 14

Let (Ω, P) be a probability space.

Prove or disprove:

(a) For all events A, B ⊆ Ω: If P(A) = P(A ∩ B) then P(B) = P(A ∪ B)

(b) For all events A, B ⊆ Ω with P(A), P(B) > 0: If P(A|B) > P(A) then P(B|A) > P(B)

Problem 15

Suppose we roll n fair, six-sided dice.

Let X be the random variable that indicates the maximum value of all dice.

(a) For m ∈ [1, 6] what is the probability that X ≤ m?

(b) In terms of n, what is the expected value of X?