Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

CIS5371 – Cryptography

Fall 2023

Scribe 2: Real Attacks on AE Schemes

2.1    ChopChop Attack on WiFi Security

WEP  construction.   The WEP construction for WiFi security is given in Figure 2.1.   It’s based on the streamcipher RC4.   WEP  is  an instance of the encrypt-with-redundancy paradigm.   Specifically,  to encrypt a message M with IV ∈ {0, 1}24 , one first appends some CRC32 checking to M to obtain a string X ← M∥CRC(M), generates a one-time pad P from RC4(K, IV), and then outputs IV∥(X ⊕ P).

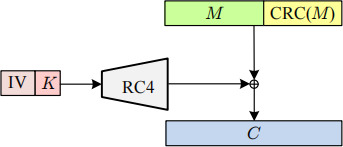
Figure 2.1: The WEP construction

Attack model.  We now describe a realistic scenario in which WEP is broken.  Under our situation, an adversary observes a ciphertext C that a user sends to an access point, and wishes to recover the underlying message.  The adversary will use the access point as a decryption oracle, querying several fake ciphertexts. For each query Dec(C* ), the decryption oracle indicates whether the ciphertext C*  is valid, but nothing beyond it. That is, if C*  is valid, the adversary doesn’t get to know the corresponding decrypted message.

ChopChop attack on WEP. Understanding the ChopChop attack for WEP requires some knowledge of finite-field multiplication. Here we describe how to attack the following variant of WEP: instead of appending CRC(M) to the message M, we will append the parity bit parity(M), the xor of all the bits of M.  For example, if M = 1011 then parity(M) = 1.  For simplicity, assume that this variant allows encrypting the empty string ε, with parity(ε) = 0.  The parity bit is a weak form of redundancy checking:  if there’s one bit flip in M∥parity(M) then one can detect that.

Suppose that the secret M = M1 ··· Mm , where each  |Mi |  = 1.  Initially, the adversary queries Enc(ε), where ε is the empty string, to receive a ciphertext C0.  Note that now the adversary knows m, by observing the length of the ciphertext C0 .   It then chops the last bit of C0  to obtain a string C1 , and queries C1 to the decryption oracle.  If the answer of the decryption oracle is 1 then Mm   = parity(M1 ··· Mm −1).  In other words, M1 ⊕ ··· ⊕ Mm  = 0.  Otherwise, if the answer of the decryption oracle is 0 then we must have M1 ⊕ ··· ⊕ Mm  = 1. In other words, we have obtained M1 ⊕ ··· ⊕ Mm . By repeating the process above for “ciphertext” C1  (instead of C0 ), we obtain M1 ⊕ ··· ⊕ Mm −1, and so on.  At the end, we have a system of m linear equations of the variables M1 ,..., Mm , which we can solve to recover M1 ,...,Mm .

Dec(C), if the ciphertext C is valid then the game returns 1 to the advesary, but the adversary doesn’t get to see the decrypted message. Otherwise the game returns 0. Define

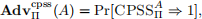
where game CPSS is defined in Figure 2.2.

Figure 2.2: Game defining CPSS security.

The CPSS notion captures the following real-world scenario.  In this setting, Alice first visits a legitimate website bank.com.  Her browser then shares a secret cookie M with this website, and embeds this in ev- ery request it sends to  bank.com.   Suppose  that  later  Alice  is  tricked  into  visiting  a  malicious  website attacker.com. This site sends a Javascript program to the broswer, requesting some resource from bank.com. The browser will correspondingly send an encrypted HTTP GET request to bank.com.  In other words, it sends C —$  εK (PIM) with a prefix P that the adversary can partially control.  The adversary then can intercept this request, replace the ciphertext with another C′ of its choice, and observe the error message from bank.com.

Attacking CPSS security of TLS encryption.  For simplicity, suppose that the byte length of M is a multiple of 16.  Let M = M1 M2 ... Mm , where each |Mi | = 16. We now recover the first block M1  of M; the same method can be used to recover any block of M.

We first recover the last byte of M1. Let ε denote the empty string. The adversary first queries Enc(ε), asking for an encryption of M. It then gets a CBC ciphertext C = C0 C1 ··· Cm+2  for M1 ··· Mm ITIpad(M), where T — FK ′ (M) and C0  is a random IV. Now modify the last block of C, replacing Cm+2  by C1 .  Let C′ be the resulting ciphertext, and query C′ to Dec.  Recall that in the implementation of Dec, the first step is to use

CBC on key K to decrypt C′ , resulting in M1 I···IMm ITIV , where V = Cm+1⊕EK(−)1 (C1 ) = Cm+1⊕M1 ⊕C0 .

See Figure 2.3 for an illustration.

After CBC-decrypting C′ to get X — M1 ··· Mm ITIV , one would need to look at the last byte of V to know how many bytes we need to truncate from X, before doing a tag comparison to check for validity.  Note that (1) if the last byte of V encodes 15 then the ciphertext C′ will be deemed valid, and (2) if the last byte of V is not 15 then it’s unlikely that C′ is valid.  Hence by observing the output of the decryption oracle, the adversary can tell if the last byte of M1 ⊕ C0 ⊕ Cm+1  is the encoding of 15.  Hence with probability about 1/256, one can find the value of the last byte of M1 .

By repeating the whole process above, the adversary can check if the last byte of M1  is the same as the last byte of another randomly chosen IV. If the adversary iterates t times then it can find the exact value of the last byte of M1  with probability around 1 — (1 — 1/256)t  ≥ 1 — e −t/256 .

So far we’ve learned just the last byte of M1 .  To learn the second last byte of M1 , instead of querying

Enc(ε), we would query Enc(08 ), asking for encryption of 08 IM.  Let the answer be C0(′) ··· Cm(′)+2 .  Then,

send C0 ··· Cm+1C1(′) to the decryption oracle.  (Note that the all blocks except the last one are from the old

ciphertext of M, not 08 IM.)  In this process, we’ll learn the last byte of the first block of 08 IM, which is exactly the second last byte of M1. We can do the same trick to learn any other byte in M1 .

A fix and its new problem.  After the security disaster of TLS encryption, here’s what people actually tried to fix it.  Now if you need to pad p bytes, every single byte must encode p — 1.  In decryption, after

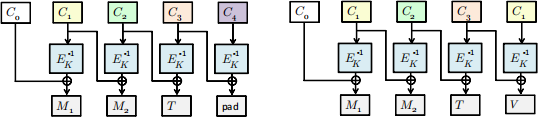
Figure  2.3:    Illustration  for  the  case  m   =   2  when  we  first  make  an  encryption  query  on  message M  =  M1 ··· Mm   to  get  ciphertext  C  =  C0 C1 ··· Cm+2,  and  then  make  a  decryption  query  on  C′ = C0 C1 ··· Cm+1C1 .   On the right is the CBC-decryption of C′ for Dec(C′ ).   For comparison, on the left is what would happen for the CBC-decryption of C.

CBC-decryption, you need to check if the padding is well-formed. If yes, then we’ll do the tag checking.

Now there are two possible reasons that we might reject a ciphertext as invalid:  (1) bad padding, and  (2) bad tag.  Some implementations actually explicitly tell users if their ciphertexts fall into  (1) or (2).  While this might be a good software engineering practice elsewhere, here it’s a security issue.

Now suppose that for the CPSS attack, M = M1 ··· Mm  with m ≥ 2.  Let’s try to recover the last byte of, say M2. The adversary first queries Enc(ε) to get a ciphertext C0 C1 ··· Cm+2  of M.  Let B be an arbitrary 16-byte string, and query Dec(C′ ), with C′ ← C0 ∥(C1 ⊕ B)∥C2. After the CBC-decryption of C′ , the last

block of the decrypted string will be (C1 ⊕ B) ⊕ EK(−)1 (C2 ) = M2 ⊕ B. If the last byte of M2 ⊕ B encodes 0

then we would receive an error for bad tag.  Otherwise, it’s likely that we would receive an error for bad padding. By trying this for many different B’s, eventually we’ll recover the last byte of M2 .

You might think that to fix the bug above, one should simply return the same error signal for both (1) and (2), but even then the problem still remains. For a naive implementation, if you have a bad padding then you’ll immediately reject the ciphertext without checking the tag, and if you have a well-formed padding, you’ll do a MAC for tag comparison.  But then there’s quite a difference in the running time between the two types of error, and thus an adversary can still tell what kind of error it has.  It requires some expertise to do a constant-time implementation to ensure that for both types of error, the running time is the same, especially when one also runs some compiler optimizations.