MATH360 Applied Stochastic Models SPECIMEN CLASS TEST 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH360
Applied Stochastic Models
SPECIMEN CLASS TEST 2
Section A
A1. Imagine you have a coin such that the probability of getting a head is random. More precisely, it is equal to P, where P is an Uniform(0, 1) random variable, i.e., P has a probability density function given by
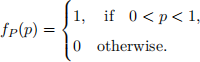
Let the (random) variable Z be the number of coin tosses until head is obtained (recall that coin tosses are independent). Suppose that the conditional distribu-tion of Z given that P = p ∈ (0, 1) is Geometric(p), that is,
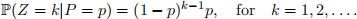
(a) Compute the distribution of Z, i.e., compute P(Z = k) for k = 1, 2, . . . .
Hint: You can use without proof that
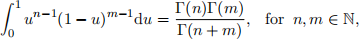
where Γ(n) = (n − 1)! is the so-called gamma function.
(b) For k = 1, 2, . . . , find the distribution of P given Z = k, that is, FP|Z=k (p) = P(P ≤ p|Z = k), for p ∈ R.
Section B
B1. Joe and Love both received soap bubble machines for Christmas. The machines emit bubbles according to independent Poisson processes with intensities 3 and 2 (bubbles per minute), respectively. Suppose they turn them on at the same time. Find the probability that Joe’s machine produces the first bubble (justify your answer formally).
Section C
C1. Imagine a population of N + 1 individuals, some of whom have a certain infection that spreads as follows. Contacts between two members of this population occur following a Poisson process having rate θ > 0. When contact occurs, it is equally likely to involve any of the 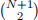 pairs of individuals in the population. If contact involves an infected and a noninfected individual, then the noninfected individual becomes infected. Once infected, an individual remains infected throughout. Suppose that we model the number of infected individuals as a simple birth process (Xt
, t ≥ 0). More precisely, Xt denotes the number of infected individuals at time t ≥ 0, and X0 = 1.
pairs of individuals in the population. If contact involves an infected and a noninfected individual, then the noninfected individual becomes infected. Once infected, an individual remains infected throughout. Suppose that we model the number of infected individuals as a simple birth process (Xt
, t ≥ 0). More precisely, Xt denotes the number of infected individuals at time t ≥ 0, and X0 = 1.
(a) Compute the birth rates (λk)k≥1 of (Xt , t ≥ 0).
(b) Show that (Xt , t ≥ 0) is not explosive.
(c) Assume now that X0 = N (i.e., there is exactly one noninfected individual) and compute E[Xt ], for t ≥ 0.
Section D
D1. Consider a population in which each individual gives birth to exactly one new individual after an exponential time of parameter λ > 0, independently and re-peatedly. This population suffers catastrophic events that cause the death of the entire population after an exponential time of parameter µ > 0, independently of the births events. Nevertheless, new individuals can immigrate into the pop-ulation. To be precise, a new individual immigrate into the population after an exponential time of parameter θ > 0 independently of the birth and the catas-trophic events. Suppose that we model the number of individuals alive in the population as a continuous-time Markov chain (Xt , t ≥ 0) by letting Xt be the number of individuals alive at time t ≥ 0.
(a) What is the state space S of (Xt , t ≥ 0)? Compute also the Q-matrix Q = (qi,j )i,j∈S of (Xt , t ≥ 0).
(b) Draw a diagram to represent the behaviour of (Xt , t ≥ 0).
(c) Compute the transition matrix Π = (πi,j )i,j∈S of the underlying jump chain of (Xt , t ≥ 0).
2023-11-11