COMP5930M Scientific Computation Coursework 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
School of Computing: assessment brief
Module title
Scientific Computation
Module code
COMP5930M
Assignment title
Coursework 1
Assignment type and description
Coursework assignment
Rationale
TBA
Weighting
20% of total mark
Submission dead-line
November 20th 2023 at 10:00
Submission method
Turnitin submission through Minerva
Feedback provision
Feedback provided on Minerva
Learning outcomes assessed
(i) Formulate and solve systems of nonlinear equations to solve challenging real-world problems arising from engineering and computational science; (ii) Analyse a given nonlinear equation and choose and implement the best numerical method for its solution; (iii) Implement algorithmic solutions to solve computational differential equation problems based on mathematical theory.
1. Assignment guidance
Provide answers to the two exercises below. Answer both exercises.
2. Assessment tasks
Exercise 1: Consider the nonlinear equation
f(x) = − cos(x) + x3 + 2x2 + 1 = 0.
(a) How many real solutions does this equation have in the interval [−3, 1]? You can use e.g. graphical analysis [2 marks].
(b) Analyse each real solution x ∗ ∈ [−3, 1] and determine:
i. What is the converge order of Newton near that solution? Justify your answer by appealing to the theory of Newton’s method and properties of the function f.
ii. Apply the Newton method (Tutorial 1) to find a computa-tional approximation from an appropriate initial guess x0 to a tolerance of tol = 10−6 . Comment on whether the conver-gence behaviour observed matches the theory.
iii. Can the bisection method converge to the solution from some initial bracket [xL, xR]? Justify your answer by appealing to the theory of the bisection method and properties of f. [10 marks]
(c) Implement Dekker’s algorithm as described in Lecture 4 in a python subroutine dekker.py following the same implementation as the Newton’s method example given in the Tutorials:
def dekker( fnon, xbounds, tol, maxk )
where xbounds contains the intial bracket endpoints xL,xR. In-clude the source code in your answer. [6 marks]
(d) Use Dekker’s algorithm from the initial bracket [−3, 1] to a toler-ance of tol = 10−6 . Use the graph estimation method of Tutorial 2 to approximate the convergence order of Dekker’s method based on these data [2 marks].
Exercise 2: Consider the solution of the nonlinear system of equations:
find (x, y) ∈ R 2 s.t.
F1(x, y) = x 2 + 2y 2 + sin(2x) = 0
F2(x, y) = x 2 + cos(x + 5y) − 1.2 = 0 (1)
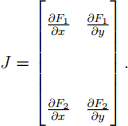
(a) Derive the analytical formulas for the four elements of the Jaco-bian matrix [4 marks]:
(b) Plot the isocontours of the function φ(x) := |F(x)| within the square (x, y) ∈ [−2, 2] × [−2, 2] . How many local minima does the function φ appear to have in this region? Which of the minima are actual solutions to equation (1)? [4 marks]
(c) Solve the problem (1) using the gradient descent method using a fixed step size of λ = 0.01 and starting from the initial guess (x0, y0) = (−2, −1) and a stopping tolerance of tol = 10−2 and maximum number of iterarions maxit = 20. Report the conver-gence of the residual and plot the iterates (xk, yk) in the (x, y) plane for k = 0, 1, 2, . . .. What do you observe? [3 marks]
(d) The gradient descent method can be modified include momen-tum to improve the convergence and avoid getting stuck in local minima. In the momentum version, the gradient step is replaced by:
dk = γdk−1 + 2JTF,
xk+1 = xk − λdk
where λ is the step-size and γ ∈ (0, 1) is the momentum constant. Modify the existing gradient descent solver to implement the mo-mentum version. Include a code listing showing the changes you have made.
Solve problem (1) using the gradient descent method with mo-mentum using a fixed step size of λ = 0.01 and starting from the initial guess (x0, y0) = (−2, −1) and a stopping tolerance of tol = 10−2 and maximum number of iterations maxit = 50. Use three different values of the momentum constant: γ = 0.3, γ = 0.5 and γ = 0.8.
Plot the iterates (xk, yk) in the (x, y) plane for k = 0, 1, 2, . . . for the three different momentum constant values. What do you observe in each case? [9 marks]
3. General guidance and study support
The MS Teams group for COMP5390M Scientific Computation will be used for general support for this assignment. If your question would reveal parts of the answer to any problem, please send a private message to the module leader on MS Teams instead. You can also use the tutorial sessions to ask questions about coursework.
4. Assessment criteria and marking process
Assessment marks and feedback will be available on Minerva within three weeks of the submission deadline. Late submissions are allowed within 14 days of the original deadline providing that a request for an extension is submitted before the deadline. Standard late penalties apply for submissions without approved extensions.
5. Presentation and referencing
When writing mathematical formulas, use similar notation and sym-bols as during the lectures and tutorials. Hand-written sections for mathematical notation are acceptable but need to be clearly readable.
You may assume theorems and other results that have been presented during lectures and tutorials as known. Any other theorems need to be cited using standard citation practice.
6. Submission requirements
This is an individual piece of work. Submit your answers through Tur-nitin as one PDF document (generated either in Word or with LaTeX). You may use hand-written and scanned pages for mathematical formu-las, but these need to be clearly legible and the document must contain at least some typeset text or Turnitin will reject it. All submissions will be checked for academic integrity.
7. Academic misconduct and plagiarism
Academic integrity means engaging in good academic practice. This involves essential academic skills, such as keeping track of where you find ideas and information and referencing these accurately in your work.
By submitting this assignment you are confirming that the work is a true expression of your own work and ideas and that you have given credit to others where their work has contributed to yours.
8. Assessment/marking criteria grid
Total number of marks is 40, divided as follows:
Exercise 1 (Newton and Dekker’s methods): 20 marks
Exercise 2 (Gradient descent with momentum): 20 marks
2023-11-11