MATH360 Applied Stochastic Models SPECIMEN CLASS TEST 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH360
Applied Stochastic Models
SPECIMEN CLASS TEST 1
Section A
A1. Imagine you have a coin such that the probability of getting a head is random. More precisely, it is equal to P, where P is a Beta(2, 2) random variable, i.e., P has a probability density function given by
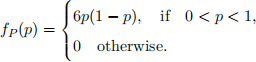
For n ∈ N, let the (random) variable Xn be equal to the number of heads after n tosses (recall that coin tosses are independent). Suppose that the conditional distribution of Xn given that P = p ∈ (0, 1) is Binomial(n, p).
(a) Compute the distribution of Xn, i.e., compute P(Xn = k), for k = 0, 1, . . . , n.
Hint: You can use without proof that
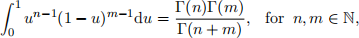
where Γ(n) = (n − 1)! is the so-called gamma function.
(b) Compute P(Xn+1 = n + 1|Xn = n) and show that
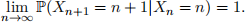
Answer the following question: Is the probability of another head large or small given that we know that there were many heads in a row?
Section B
B1. A particle source A emits one particle at a time, according to a Poisson process with an intensity of two particles a minute. Another particle source B emits two particles at a time, according to a Poisson process with an intensity of one particle a minute. The sources are independent of each other. Suppose you begin to observe the sources at time zero. Compute the probability that source A has emitted two particles before source B has done so (justify your answer formally).
Section C
C1. Imagine a population of N + 1 individuals suffering an epidemic that spreads as follows. Every pair of individuals with different states (i.e., infected or nonin-fected) gets in contact after an exponential time of parameter θ > 0 and then the nonifected becomes infected and remains so forever. The times associated with the pairs are independent. Suppose that we model the number of infected individuals as a simple birth process (Xt , t ≥ 0). More precisely, Xt denotes the number of infected individuals at time t ≥ 0, and X0 = 1.
(a) Compute the birth rates (λk)k≥1 of (Xt , t ≥ 0).
(b) Show that (Xt , t ≥ 0) is not explosive.
(c) Assume now that X0 = N (i.e., there is exactly one noninfected individual) and compute E[Xt 2 ], for t ≥ 0.
Section D
D1. Consider a biological population in which each individual gives birth to exactly one new individual after an exponential time of parameter λ > 0, independently and repeatedly. Furthermore, each individual dies after an exponential time of parameter µ > 0, independently of the births and the other individuals. In addition, there is an exponential rate of increase θ > 0 due to immigration (i.e., a new individual immigrates into the population after an exponential time of parameter θ independently of the birth and death events). However, immigration is not allowed when the population size is N or larger. Suppose that we model the number of individuals alive in the population as a continuous-time Markov chain (Xt , t ≥ 0) by letting Xt be the number of individuals alive at time t ≥ 0.
(a) What is the state space S of (Xt , t ≥ 0)? Compute also the Q-matrix Q = (qi,j )i,j∈S of (Xt , t ≥ 0).
(b) Draw a diagram to represent the behaviour of (Xt , t ≥ 0).
(c) Compute the transition matrix Π = (πi,j )i,j∈S of the underlying jump chain of (Xt , t ≥ 0).
2023-11-11