CS 335 - Fall 2023: Assignment 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CS 335 - Fall 2023: Assignment 2
Due: Friday, Oct 27, 2023, 23:59pm.
Submit all components of your solutions (written/analytical work, code/scripts/notebooks, igures, plots, etc.) to CrowdMark in PDF form in the section for each question.
You must also separately submit a single zip ile containing any and all code/notebooks/scripts you write to the A2 DropBox on LEARN, in runnable format (that is, .ipynb).
For full marks, you must show your work and adequately explain your logic!
1. (15 marks) Option pricing using a binomial lattice.
Coding: Develop Jupyter/Python code for pricing European and American options, of both put and call type, using a binomial lattice. Use the lattice parameters for the no-arbitrage lattice, as described for example in Section 3.2 of the course notes (and in lectures). For this question, you do not need to apply smoothing of the payof.
Your code should be vectorized so that there is only one explicit for loop over the timesteps (i.e., no for loops over vector entries within one timestep). See Section 3.5 of the course notes for hints on how to proceed. Also, your code should take only O(N) storage, NOT O(N2). That is, do not store data for the whole tree at once, but rather data for one or two columns at a time. In the American case, ensure that you compute the payof at each time step using vector operations; this will require determining/knowing the vector of stock prices for that time/column.
Test your code for European put/call options code by using the data in Table 1 below. Compare with the exact analytical solution values given by the function blsprice provided with the assignment. (blsprice is designed to mimic the Matlab function of the same name, so you can ind details on it here: https://www.mathworks.com/help/inance/blsprice.html)
Generate text tables showing the option value VΔt(S0(0) , 0) (for both puts and calls) as a function
of Δt. Start of with 500 timesteps (i.e., Δt = T/500), and then repeat the process doubling the number of timesteps, i.e., 1000, 2000, . . . 8000, timesteps. You should expect to see your results converging towards the exact solution value. Your tables be structured roughly like Table 2 (but you do not need to make fancy borders - just rows of text is ine). Your table should also show the exact (blsprice) value for comparison (where available).
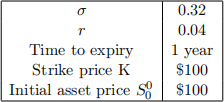
Table 1: Some typical option parameters
If Vexact is the exact price, and Vtree is the price from a lattice pricer, then it is possible to prove that
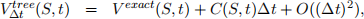 (1)
(1)
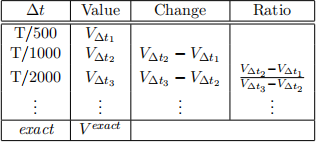
Table 2: Convergence Test
where C(S, t) is independent of Δt. Estimate (by hand calculation using the above formula)
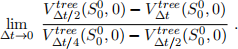 (2)
(2)
What order of accuracy does the convergence data table you generated indicate our lattice method is likely exhibiting? Does this agree with the theory above?
Next, repeat the above tests for an American put (no analytic solution available), using the data in Table 1. Show a convergence table as in Table 2 (but without the exact solution).
2. (5 marks) Smoothing the Payof.
In this question, we consider a variant of a put option known as a digital put option. Such an
option is characterized by a strike price K and a payof according to
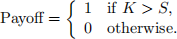
where (as usual) S is the stock value. Determine the expressions for the smoothed digital put payof in this case. You should use the same smoothing strategy as covered in the lecture (which will, of course, have to be modiied for a digital put).
3. (10 marks) Binomial lattice.
A binomial lattice is given with the properties
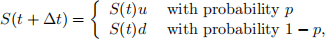
where
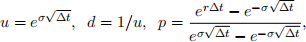
over the time interval Δt.
(a) Show that
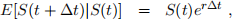
where E[ ·] is the expectation.
(b) Show that
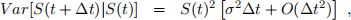
where Var is the variance. Hint: the Taylor expansion of ex is
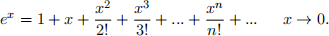
4. (8 marks) Lattice properties.
Let Cj(n) be the value of a European call option at node (j, n), obtained using a no-arbitrage lattice. Likewise, let Pjn be the value of a European put option at node (j, n), obtained using a no-arbitrage lattice. Assume that Pjn and Cj(n) both have the same strike price K, are based on the same underlying stock S, and have expiry time T = NΔt. Show that
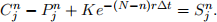 (3)
(3)
This is a discrete version of what is called put-call parity.
Hint: Induction is often useful for understanding lattices, and that is the case here as well. Work backwards from the expiry time (i.e., column N in the lattice) and use the rules that deine the relationships between S at adjacent timesteps, and likewise for the option price V at adjacent timesteps (in this case we have used C or P rather than V to distinguish the two types of options, but the update rule remains the same).
5. (8 marks) Dynamic Programming.
Consider the following game. You are given a fair ive-sided die, with faces f0, 1, 2, 3, 4g. You can roll the die, and obtain a payof equal to the value shown on the die, or you can choose to roll again. Note that if you choose to roll again, you can only get the new payof or roll again. You can roll the die up to three times. You must pay s1.4 for the irst roll, s1.05 for a second roll, and s0.85. for a third roll. You pay only for the rolls you choose to take, and get no money back if you move onto the next roll. What is your expected gain, assuming you were to behave optimally at each step? (Hint: this is somewhat similar to the marriage problem we looked at in lecture. Use dynamic programming; i.e., work backwards from the last roll!)
Work this out manually, i.e., you do not need to write or run any code here.
2023-10-28