Due Tuesday, October 31 at 11:59pm via Gradescope

• Make sure to put your name on the first page.  If you are using the LATEX template we provided, then you can make sure it appears by filling in the yourname command.

• This assignment is due Tuesday, October 31 at 11:59pm via Gradescope. There is a 24-hour grace period for late assignments. Make sure to submit something well before the deadline.

• Solutions must be typeset. If you need to draw any diagrams, you may draw them by hand as long as they are embedded in the PDF. We recommend that you use LATEX, in

which case it would be best to use the source file for this assignment to get started.

• We encourage you to work with your classmates on the homework problems, but also urge you to attempt all of the problems by yourself first. If you docollaborate, you must writeall solutions by yourself, in your own words. Do not submit anything you cannot explain. Please list all your collaborators in your solution for each problem by filling in the yourcollaborators command.

• Finding solutions to homework problems on the web, or by asking students not enrolled in the class is strictly forbidden.

Problem 1.  They’re greedy and they’re kooky, mysterious and spooky (4+4+8 = 16 points)

It is Halloween night and almost time for the trick-or-treaters to arrive at the Addams Family Mansion! Of course, Wednesday and the family will be up to their usual haunts, so they won’t be able to man the door. Fortunately, the Itt cousins are in town and are willing to lend their services. There are n cousins in total and each cousin informs Wednesday of when they would be able to work the door. Wednesday’s job is to figure out which cousins to select so that the door is always tended to by at least one of the cousins (overlap is okay) and asfew cousins are selected as possible (so that the rest of them can join the Addamses in their shenanigans!). Wednesday has been too busy solving mysteries to learn algorithms, so she has asked you to help her out!

To formalize, trick-or-treaters may arrive at any time between s and t.  Each of the n Itt cousins provides a start and end time of when they are able to tend to the trick-or-treaters. This data is in the form of intervals, where cousin i (i ∈ {1, . . . , n}) can work the door from [si, ti]. You should tell Wednesday a set of cousins C ⊆ {1, . . . , n} such"i∈C [si, ti] covers all of [s, t] and |C| is minimized. This means that for any time a ∈ [s, t], there is a cousin i ∈ C such that a ∈ [si, ti]. You can assume that such a set C exists.

To help Wednesday out, construct a greedy algorithm that takes as input the numbers s, t, s1, t1, . . . , sn, tn and outputs a set C which meets the constraints stated above. Your algorithm should run in time O(n2).

Here is an example input with 9 cousins. One optimal solution is C = {3, 4, 9}.

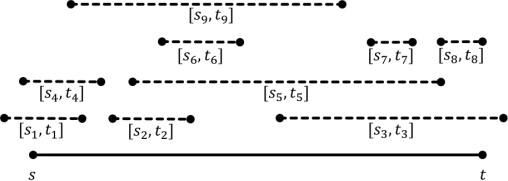
(a) Describe your algorithm in pseudocode. Provide a few sentences describing your algo- rithm.

(b) Analyze the running time of your algorithm.

(c) Prove that your algorithm finds a set of cousins C of minimum size to tend to the door for the entire [s, t] period.

Problem 2.  Greedy algorithms are really very simple, all you’ve got to do is see what looks best, and let yourself have it! (4+4+8 = 16 points)

After helping Wednesday and the Addamses out, your assistance is requested in Halloween- town! In particular, they would like your assistance decorating the haunted houses on Spooky Street. There are n houses in total, and they are all on the same side of the road (naturally, there is a graveyard on the other side of Spooky Street). The houses are conveniently numbered from 1 to n.

The haunted houses are set to be decorated with pumpkins from the local pumpkin patch. However, the residents of Spooky Street are up in arms about fairly dividing the pumpkins to houses. After much debate, the following resolution is met:

Pumpkin Resolution: Each haunted houses should get at least one pumpkin, and any pair of neighboring houses i and i +1, if one house has more candy to pass out than the other, then that house should get more pumpkins than the other1 .

Haunted house i has c [i] pieces of candy. You need to figure out the minimum number of pumpkins needed to decorate the haunted houses according to the Pumpkin Resolution. To do so, you will develop an O(n) time algorithm using a greedy technique.

(a) Consider the following verison of the Pumpkin Resolution:

Partial Pumpkin Resolution: Every haunted house should get at least one pumpkin, and for neighboring houses i and i + 1, if there are more pieces of candy at house i + 1, then i +1 should receive more pumpkins than i.

Write (in pseudocode) a O(n) greedy algorithm that, given input array c, determines a way to distribute the pumpkins to the houses using the minimum number of pumpkins, while satisfying the Partial Pumpkin Resolution. The output of your algrotihm should be an array p, where p [i] is the number of pumpkins received by house i.

(b) Justify the correctness of your algorithm. Your justification does not need to belong or formal, just convincing.

(c) We now consider the original problem with the Pumpkin Resolution. Extend your algo- rithm from part (a) to design an O(n) time algorithm that, given input array c, determines a way to distribute pumpkins to the houses such that the Pumpkin Resolution is followed with the minimum number of pumpkins being used 2 .

Write your algorithm in pseudocode.  Justify the correctness of your algorithm.  Your justification does not need to belong or formal, just convincing.

Problem 3.  Graph Representations and Exploration (4+3+3+4+2+2 = 18 points)

This problem is about the following graph, as well as general graph questions.

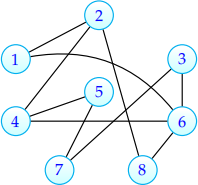
(a) Identify a cycle of length 7 in the graph. Identify a cycle of length 4 in the graph. If we made this graph directed by adding an orientation to each edge arbitrarily (e.g. by flipping a coin), is there necessarily a directed cycle corresponding to each cycle in the original graph? Justify your answer.

(b) A trail is a path where all of the edges are distinct. A simple pathis a path where of the vertices are distinct. Which of these can be longer than the other? Justify your answer. Provide an example which makes your argument on this graph.

(c) What are the maximum (Δ) and minimum (δ) degrees of nodes on this graph? Consider the ratio between these values, r = Δ(G)/δ(G), in general.  What are upper bound and lower bounds we can always make on r, in any connected simple graph G with n ≥ 1. Justify your answer.

(d) Is this graph connected?  If so, what is the minimum number of edges that need to be deleted to make it not connected? If no, what is the minimum number of edges that need to be added to make it connected? Justify your answer.

How could we take the given graph G and create a directed graph G′ on the same set of nodes, where there is a path from u to v in G if and only if there is path from u to v in G′? Could we take a general directed graph G′ and create an undirected graph G on the same set of nodes, where there is a path from u to v in G if and only if there is path from u to v in G′? If so explain how to do this. If not, explain why not (a counterexample would be sufficient).