MAST30001 Assignment 2 - Part 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MAST30001 Assignment 2 - Part 2
Due 11.59pm, Wednesday, October 18
Question 1 [25 Marks]
Question 1 appears in Part 1 of Assignment 2, which you can download separately from the MAST30001 webpage.
Question 2 [8 Marks]
The Yule-Furry process is a pure birth continuous-time Markov chain on the state space {1, 2, . . .} with generator
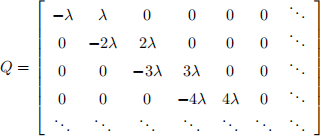
where λ is a positive constant known as the splitting rate.
(a) For n ∈ {1, 2, . . .} and t ∈ R+, let Pn(t) be the probability that a Yule-Furry process with splitting rate λ is in state n at time t, given that it starts in state 1. Write down the Kolmogorov Forward Differential Equations for Pn(t).
(b) Use mathematical induction to show that the solution to these equations is
Pn(t) = e−λt (1 − e−λt )n−1 .
Question 3 [8 Marks]
Consider an M/M/m/m queue, that is a queue with Poisson arrivals with rate λ, exponentially- distributed service times with rate µ, m servers and no waiting room. Such a queue is known as an Erlang Loss System after the founder of queueing theory A.K. Erlang. In a 1917 paper, he used such a queueing system to model a traditional telephone exchange with m circuits.
(a) Write down the generator for a CTMC model for the number Xt of customers this queue.
(b) Derive the stationary distribution of Xt. (NB. You will not be able to simplify the ex- pression for π0 beyond a finite sum).
(c) Hence write down an expression for the probability B that the system is full. B is known as the blocking probability because it is the probability that a customer who wishes to make a call will not gain access to the exchange.
(d) What is the expected time D that a customer who gains access to the queue spends in the system?
(e) (A question that requires a bit of intuition.) Let NA(t) be the number of customers that are admitted to the system during [0,t]. The process NA(t) is not a Poisson process. In fact, it is not even a renewal process because the distribution of time until the next cus- tomer is admitted depends on how many customers were there when the current customer arrived.
However the long-term rate γ = limt→∞ NA(t)/t does exist with probability 1. Conjecture a value for γ .
(f) Use your answers from parts (d) and (e) and Little’s Formula to derive an expression for the mean number in the system.
Question 4 [9 Marks]
Thinking again about the M/M/m/m queue from Question 3, we turn our attention to the process NB(t) of blocked calls. A customer is blocked when there are m customers in the queue and a further customer tries to gain access. We can model this situation by introducing a
modified CTMC X(-)(t) with an extra state (m,⋆) to indicate that a customer has arrived when
the state is m. The transition rate from state m to state (m,⋆) is λ, while the transition rate from state (m,⋆) to state m − 1 is mµ, indicating a service has occurred when the state is (m,⋆). When the state is (m,⋆), it is possible that further customers arrive and are blocked. This occurs in a Poisson process at rate λ .
(a) Observing that the time τ until the next customer is blocked is the time until either
❼ a-Poisson arrival occurs while the state of X(-)(t) is still (m,⋆), or
❼ X(t) leaves state (m,⋆) (necessarily to state m − 1), and then returns to (m,⋆),
use the Markov property to explain why NB(t) is a renewal process.
(b) For j = 0 to m, let Tj be the expected time until Xt hits state (m,⋆) given that it starts in state j. Write down a set of equations that are satisfied by the Tj .
(c) Explain why E[τ] satisfies the equation
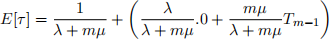
(d) For the case where λ = µ = 1 and m = 2, solve the equations in part (b) and hence evalute E[τ].
(e) What is limt→∞ NB(t)/t?
(f) Use this result to verify your conjecture in Question 3(e) for this example.
2023-10-16