Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

University of Toronto

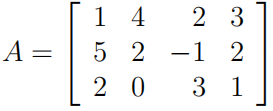
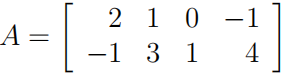
(ii) Does it admit a pure-strategy saddle-point equilibrium solution?

3. Consider a two-player zero-sum matrix game with m × n cost matrix A = [ajk], j ∈ {1, . . . , m}, k ∈ {1, . . . , n}, and assume the pure (saddle-point) value of the game is J ∗ .

Consider the game with cost matrix B = [bjk],where bjk = ajk + q, for j ∈ {1, . . . , m}, k ∈ {1, . . . , n}. Prove that this game has value J ∗ + q and that the optimal strategies of the players are unchanged.

4. Consider a two-player zero-sum matrix game with m × n cost matrix A = [ajk] and assume players use mixed strategies denoted by x ∈ ∆1 and y ∈ ∆2, respectively. Let (x 0 , y0 ) ∈ ∆1 × ∆2, (x 00 , y00 ) ∈ ∆1 × ∆2 be two mixed-strategy saddle-point (NE) equilibria pairs/points. Prove that (x 0 , y00 ) and (x 00 , y0 ) are also equilibria pairs (hence are interchangeable).

Show and justify all your steps.

5. Consider the statement at the end of Step 1 in the proof of Theorem 2.10:

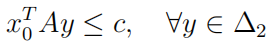
from which (b) follows.”

Fill in and justify the missing steps of the logical argument to prove that indeed (b) follows from the inequality.