Question 1/4: Naive Bayes: discrete feature values

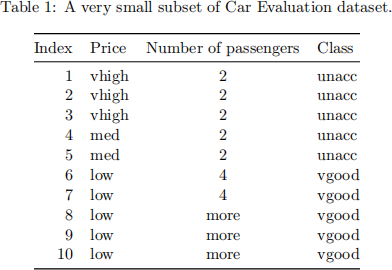
Consider a small subset of Car Evaluation dataset in Table 1 as the training dataset.

1.  Construct a naive Bayes classifier!  (Apply the Laplacian correction if necessary)

2.  Calculate the training F1-score of the classifier constructed in Question 1.1!

3.  (True/False) For naive-Bayes classifiers, we assume that the distributions of the input vari- ables x1 , x2 ,..., xf  are independent, where xi  denotes the i-th feature for i = 1, 2,...,f, and f denotes the number of features.

Question 2/4: Naive Bayes: continuous feature values

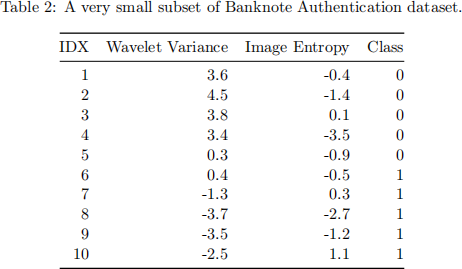
Consider a small subset of the banknote authentication dataset in Table 2 as the training dataset.

1.  Construct a naive Bayes classifier!

Here, the class-conditional densities are assumed to be Gaussian distributions whose proba- bility density function f(x) is given by

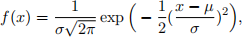
where µ and σ denote the mean and standard deviation, respectively.

2.  Calculate the training F1-score of the classifier constructed in Question 2.1!

3.  Recapitulate the number of parameters to estimate for the classifier constructed in Ques- tion 2.1!   Then,  state  a general expression  about the number of estimated parameters in terms of the number of classes and the number of features!

Question 3/4: k-NearestNeighbors (k-NN)

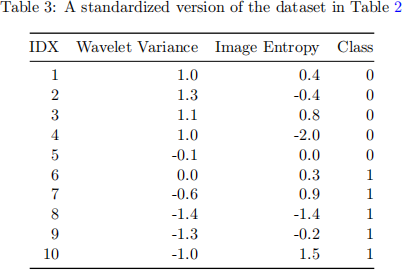
Consider a dataset in Table 3 as the training dataset.

1.  Construct a k-NN classifier using the Manhattan distance function and k = 1, then calculate its training F1-score!

2.  Re-construct the above k-NN with k = 3, then re-calculate its training F1-score!

3. Why do we need to use the standardized version of the Banknote Authentication dataset, i.e. Table 3 (instead of Table 2)?