MATH1014 Mathematics and Applications 2 Assignment 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH1014
Mathematics and Applications 2
Assignment 1
Sem 2 2023
Due at 11:59 pm on Wednesday, 30 August on gradescope
The assignment will give you the opportunity to practice explaining mathematics in writing. In each case, you should explain your solution as if you were trying to help a friend who had missed this topic; be as clear as possible so that your peers could learn from your explanation. Simply providing the correct final answer without justification is not worth any credit.
Your explanation must be your own work. You may discuss the solution with classmates, but do not post this question online or copy a solution from an existing electronic or printed resource.
. Your solutions are to be submitted on gradescope. A link to the gradescope submission will be available on wattle. Your demonstrator will mark the assignments and provide feedback online.
. Late Submissions: Assignments are due on a Wednesday and solutions are provided on the Friday following or as soon as possible once all extensions have elapsed. Late submissions attract a penalty of 5% per day. No assignments are accepted after solu- tions have been posted.
. Justify your answers fully, quoting the appropriate results from the lectures, text- books or course notes (no need to reference exact page numbers).
. If you use any other sources, apart from those listed above, they should be referenced fully so that we may find them easily.
. You should produce well-structured mathematical arguments where appropriate. This generally means explaining the steps of your working (in English), rather than just writing a mess of equations. A component of your assignment mark will reflect the style and presentation of your solutions.
Question 1. Algebra (10 marks)
1. The Hermite polynomials are an important family of polynomials that describe the wavefunction of a quantum particle. The space of wavefunctions is a vector space (with complex scalars), and the full family of Hermite polynomials {Hn (x) | n > 0, n ∈ Z} form a basis for that vector space.
The first four Hermite polynomials are
H0 (x) = 1, H1 (x) = 2x, H2 (x) = 4x2 − 2, H3 (x) = 8x3 − 12x.
Show that the set H = {H0 (x), H1 (x), H2 (x), H3 (x)} of these polynomials forms a basis for the vector space P3 of polynomials of degree at most 3. (3 marks)
2. Let p(x) = 12x3 − 8x2 − 12x + 7 ∈ P3. Find the co-ordinate vector of p relative to the basis H for P3. That is, find [p(x)]H . (2 marks)
3. The Hermite polynomials can be written using something called a generating func-tion. That is, there is a formula for the nth Hermite polynomial given by

Using the first four polynomials, find a recurrence relation for the Hermite polyno- mials of the form Hn+1 = f(x)Hn (x) + g(n)Hn−1 (x) for n ≥ 1, where f and g are linear functions of x and n, respectively. Then, show that the generating function satisfies the relation you find. (3 marks)
You may use the general Leibniz rule for repeated derivatives:

Note that the terms in this series are mostly 0, and you should give a reason why.
You may also need the binomials (0(n))= 1, and(1(n))= n.
4. The complex span of all the Hermite polynomials,
spanC {Hn (x) | n > 0, n ∈ Z},
gives rise to a vector space. Is this vector space infinite-dimensional vector space? Explain your answer. (2 marks)
Question 2. Calculus (10 marks)
1. In the lectures, we skipped over showing that the function (1 + x)k was actually equal to the Taylor series
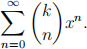 (1)
(1)
In principle, we needed to show that the remainder term vanished but this turns out to be very difficult. Instead, we can try something else:
(a) The series in (1) is some function of x, as long as it converges. Let’s call it g(x). Differentiate the function g(x), show that the resulting series g′ (x) satisfies
(1 + x)g′ (x) = kg(x),
and give its radius of convergence. Hint: you can treat the left-hand side as multiplying polynomials term-by-term. You may make use of the identities:

(4 marks)
(b) Now, introduce a new function h(x) = (1 + x)−kg(x). Show that h′ (x) = 0. (2 marks)
(c) Using the previous result, deduce that g(x) = (1 + x)k , showing that indeed this function is equal to its Taylor series. Hint: What functions have a zero derivative for all values of x where they are defined? (2 marks)
2. Using the Taylor series expansion of ex , cos(x), and sin(x), show that
eix = cos(x) + isin(x)
and deduce that eiπ + 1 = 0. (2 marks)
2023-08-25