ST301 – Actuarial Mathematics 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Online Assessment for ST301
ST301 – Actuarial Mathematics (Life)
January 10, 2023
Throughout this coursework, we will work with a given force of mortality
µx = 0.0005 + 0.00007585775 · exp(0.08749823x).
This is the same force of mortality that we used for the examples in the final Week 11 lecture. You may also wish to recall that an integration then gives
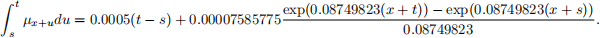
and, in particular,

To save you some time, the above functions are given to you in the R script uploaded alongside this document. The R script also contains a few other useful hints. Don’t worry if you can’t solve everything. There are lots of points to be gained by just approaching things in a sensible way.
1. [64 marks] An insurance company is about to issue a particular policy, functioning as a combined life insurance and pension for a policyholder who is currently 30 years old. The policy will be financed by a yearly premium π, which is paid continuously until the retirement age of 67 or until death, whichever comes first. A payment of 100,000 is made immediately upon death if this happens before the age of retirement. From the age of retirement (and for as long as the policyholder is alive), the policyholder receives 22,500 per year, paid continuously. You may assume that the policyholder cannot live beyond the age of 100.
(a) [15 marks] Consider a valuation basis with r ∗ = 4% and µ ∗ x = µx. Using the equivalence principle, compute the premium π ∗ corresponding to this valuation basis.
(b) [5 marks] Solve Thiele’s ODE for the reserves Vt ∗ , by solving it backwards in time from a suitable terminal condition (using the valuation basis and premium from (a)). Plot the solution.
Now suppose the policy also has the following two with-profit components: (i) any surplus that emerges before the retirement age is accummulated and paid as a single bonus immediately upon reaching the retirement age, and (ii) any surplus emerging after the retirement age is paid continuously as a cash bonus with a guarantee that the bonus payments are always non-negative. Suppose the insurance company is charging the premium π ∗ computed above. The actual interest rate r(t) is modelled as a continuous-time Markov chain. It can take three values r (1) = 2%, r (2) = 4%, or r (3) = 6%. The transition rate between any two (distinct) states is 0.4. The interest rate starts out at 4%. We assume there is no uncertainty about the mortality
(c) [20 marks] Assume the policy started exactly two years ago. The interest rate was 4% in the first year and 2% in the second year (it is still 2%). The policyholder remains alive and well. By solving a system of ODEs in R, provide a prediction for the single bonus paid at the retirement age of 67.
Hint 1: as in the lecture slides, you can set up a system of ODEs that needs to be solved backwards in time from terminal conditions. For one of the terminal conditions, you may wish to use that you solved the ODE for V ∗ in (b), so you can get the appropriate terminal condition from there.
Hint 2: you will also need to compute the past surplus L(t), by performing a numerical integration in R involving V ∗ . To do this, you can use the R function ‘approxfun’ to turn the output from the ODE solver into a function of time that you can integrate (more info in the R script).
(d) [20 marks] Now suppose the policyholder has just turned 67. By solving a system of ODEs in R, predict the EPV of the costs of the cash bonus guarantee from time t onwards, for each t = 37, . . . , 70 and each possible value of the interest rate at the given time t. You can plot the solutions or show them as a list of values. Finally, answer the following: if the interest rate is 2% when the policyholder reaches retirement, what is then the EPV of the future costs of the cash bonus guarantee at the time of retirement?
(e) [4 marks] In view of (d), what might the insurance company wish to consider when setting the premium?
2. [36 marks] Consider a unit-linked insurance with a term of 30 years. The life is currently aged 40 (at the start of the policy). The benefit is paid immediately upon death or at the end of the term. The size of the benefit is the value of the unit fund at the time of payment subject to a guarantee that the policyholder is paid a minimum of £100, 000. The yearly premium is an integer value π per year paid continuously (until payment of the benefit). Let
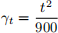
be the fraction of the premiums invested in the cash fund at time t.
(a) [2 marks] Noting that γt is increasing from 0 to 1 over the term of the policy, what could be the rationale for choosing γt to have this property?
(b) [4 marks] Let the safe interest on the cash fund be 2% and assume we are projecting a higher rate of return of 8% on the unit fund. Write down the ODEs for the values Vt and Ut of the cash fund and the unit fund, respectively.
(c) [20 marks] Let the yearly premium π be calculated based on the usual equivalence principle V30 + U30 = 100, 000. By solving the ODEs numerically using R, find the value of π. The correct value is approximately equal to an integer value, which is the value you should state (no need to worry about decimals). Finally, plot the solutions Vt and Ut for the value of π that you find.
Hint: the correct solution is somewhere between 800 and 1000. You need to find V30 and U30 for a range of values of π and confirm what value of π leads to V30 + U30 = 100, 000 (approximately).
(d) [6 marks] Suppose it is now 25 years since the start of the policy, and the policy holder is still alive and well. Up until now, the rate of return has indeed been 8%. However, it turns out that you are now forecasting a return of 3% on the unit fund for the remainder of the period. The yearly premium is contractually fixed, so it does not change from the value computed in (c). Plot the values of the cash fund and the unit for the remaining 5 years of the policy.
Note: if you did not find a value for π in (c), or if you did not get something between 800 and 1000, then you can just use π = 900 for your calculations. This is not the same as the value you are meant to find in (c), but you will also get full points using this value in (d) and (e).
(e) [4 marks] How does the new situation in (d) impact the insurance company and the policyholder? What does this mean for how to set the premium and keep reserves for unit-linked policies?
2023-08-12