ST301 – Exercises Parts II and III
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
ST301 — Exercises parts II and III
1. widow,s pension. A married couple buys a combined life insurance and widow,s pension policy specifying that premiums are payable at rate π as long as both husband and wife are alive, widow,s pension is payable at rate b (as long as the wife survives the husband), and a life assurance with sum S is due upon the death of the husband if the wife is already dead (a beneit to their dependents). The policy terminates at time n. The relevant Markov model is summarized in the picture below (the same as in the slides, with diferent transition intensities!):
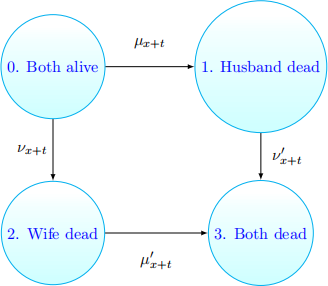
(a) Give the expressions of the transition probabilities poi(o, t) for all i = {o, 1, 2, 3} and all t = [o, n].
(b) provide Thiele,s diferential equations for the reserves vi(t) for all states i = o, 1, 2, 3, together with the corresponding boundary conditions.
2. consider two lives with ages x and g. Denote μ从+t and μg+t theirrespective mortality forces.
(a) what is the remaining lifetime of the joint life status? compute its survival probability and give the form of its force of mortality in the case when the two lives are independent.
(b) consider the following policy: a beneit B payable upon the irst death is funded by a time continuous premium whose (constant) rate π, which is paid as long as one life is alive. compute the premium using the equivalence principle.
(c) Deine the remaining lifetime T(-) of the last survivor status and compute how long is the time interval between the irst death and the last death on average.
3. A life insurance on John and paul pays death beneits as follows:
(i) 1 at the death of John if paul is alive,
(ii) 2 at the death of paul if John is alive,
(iii) 3 at the death of John if paul is dead and
(iv) 4 at the death of paul if John is dead.
The joint distribution of the lifetimes of John and paul is equivalent to the joint distribution of two independent lifetimes each age x. show that the net single premium of this life insurance is equal to 7Ac - 2Acc.
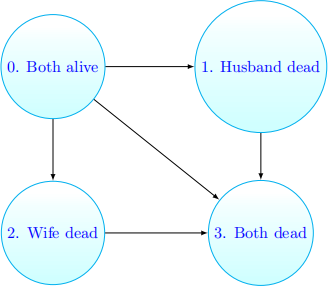
4. The igure below illustrates the common shock model. This is the joint life and last survivor model, adjusted to allow for the possibility that the husband and wife die at the same time (for example as the result of a car accident). An insurance company issues a joint life insurance policy to a married couple. The husband is aged 28 and his wife is aged 27. The policy provides a beneit of 5OOOOO immediately on the death of the husband provided that he dies irst. The policy terms stipulate that if the couple die at the same time, the elder life is deemed to have died irst. premiums are payable annually in advance while both lives are alive for at most 3O years.
Question: calculate the annual net premium using an efective rate of interest of 5% per year and transition intensities of
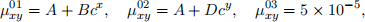
where A = O.OOO1, B = O.OOO3, c = 1.O75 and D = O.OOO35.
5. Diversiiable vs non-diversiiable risks 1 An insurer issues a portfolio of identical 5- year term insurance policies to independent lives aged 75. one-half of all the policies have a sum insured of 1OOOO, and the other half have a sum insured of 1OOOOO. The sum insured is payable immediately on death. The insurer wishes to measure the uncertainty in the total present value of claims in the portfolio. The insurer assumes an interest rate of 6% per year efective.
The following values will be very useful in the computations:
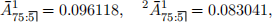
where the superscript 2 indicates that the term insurance function is evaluated using an efective interest rate of 1.o62 - 1 = o.1236 per year. They have been computed using the standard ultimate survival Model.
(a) calculate the standard deviation of the present value of the beneit for an individual policy, chosen at random.
(b) calculate the standard deviation of the total present value of claims for the portfolio assuming that 1oo contracts are issued.
(c) By comparing the portfolio of 1oo policies with a portfolio of 1ooooo policies, demon- strate that the mortality risk is diversiiable.
6. surplus 1. An insurer is ofering 3o year endowment assurance policies to lives aged 3o. The sum of 1ooooo is payable at the end of the policy or at earlier death. The policies are inanced by a continuous premium payable throughout. The policies might lapse at any time with a force o.o1 (the policyholder decides not to pay any more premiums). should that happen during the irst 2o years the company imposes a charge of 5% on the reserve and uses the remainder as a single premium for a pure endowment assurance payable at time 3o. If the policy lapses during the last 1o years the charge is not applicable, so the whole reserve is used to inance the pure endowment. In either case there is no death beneit.
(a) using a force of interest of o.o5, set up and solve the Thiele ODE for the reserves and use the terminal condition to provide an equation for the continuous premium π . Note
that you are not asked to solve that equation.
(b) provide expressions for the reserve at all times and states.
7. surplus 2. An office issued a with proits 2o year endowment assurance with a sum assured of 1ooooo. The policyholder was then aged 4o. The premium is payable continuously and is to be calculated using the mortality force μx+t, a force of interest of o.o4 and no expenses. The real force of interest is stochastic and can take the values o.o3 and o.o6. The transition rates between the two values are o.5. The real mortality force is also μx+t (hence: no mortality risk). The force of interest is o.o6 initially. The policyholder will receive all surplus in the form of a terminal bonus.
(a) The insurer wants to predict the terminal bonus. provide the relevant system of ODEs together with the corresponding terminal conditions that the insurer can solve to predict the terminal bonus.
(b) suppose that we are at time t = 5 and the force of interest has been o.o6 for the last 5 years (it still is). provide a system of ODEs (and terminal conditions) that the insurer can use to predict the terminal bonus in this case.
8. surplus 3. An office issued with proits 3o year endowment assurance policies to 3o year old lives with a sum assured of 1oo)ooo. The premium is 198o per annum payable continuously and was calculated using a force of mortality μx , where x is the life,s age, a force of interest of o.o2 and no expenses.
The real force of interest is stochastic and can take the values o.o1 and o.o4. The transition intensities between the two values are both o.5, while the initial force of interest is o.o4. The actual force of mortality is also μx at age x. The policyholders will receive all surplus in the form of a cash bonus. The emerging surplus is paid out to policyholders if it is positive and nothing is paid if it is negative.
Explain how you would calculate the expected present value of the loss the office will incur over the period of the policy.
9. unit-linked fund 1. An office issues 3o-year unit-linked endowment assurance policies to lives aged 3o. The policies are inanced by a continuous premium payable at rate π .
At any time t, half of the premium is invested in a unit fund which grows at a constant force of interest T. The remaining half is allocated to a cash fund at a null force of interest T* = o. At time t = 3o or on earlier death the policyholder will receive the accumulated amount of the fund or a guaranteed sum b = 1, whichever is larger.
There is also the possibility of surrenders which occur independently of deaths and with a constant intensity δ > o. surrenders are entitled to their share of the unit fund (without guarantees) but not to any of the cash fund.
(a) write down and solve the differential equations (with the right boundary conditions) satisied by the value U (t) of the unit fund.
(b) write down and solve in integral form the diferential equation (with the right boundary condition) satisied by the value V (t) of the cash fund.
(c) using the equivalence principle, set an equation for the premium rate π . Notice that you are not asked to solve explicitly the equation.
10. Unit-linked fund 2. An office issues 3o-year unit-linked endowment assurance policies to lives aged 3o. The policies are inanced by a premium π0 paid upfront.
At any time t = o, half of the premium is invested in a unit fund which grows at a constant force of interest T . The remaining half is allocated to a cash fund at a null force of interest T* = o.
At time t = 3o or on earlier death the policyholder will receive the accumulated amount of the fund or a guaranteed sum b = 1, whichever is larger.
There is also the possibility of surrenders which occur independently of deaths and with a constant intensity δ > o. surrenders are entitled to their share of the unit fund (without guarantees) but not to any of the cash fund.
(a) write down and solve the diferential equations (with the right boundary conditions) satisied by the value U (t) of the unit fund.
(b) write down and solve in integral form the diferential equation (with the right boundary condition) satisied by the value V (t) of the cash fund.
(c) using the equivalence principle, set an equation for the premium π0 . Notice that you are not asked to solve explicitly the equation.
2023-08-12