COMP9020 Assignment 2 2023 Term 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP9020
Assignment 2
2023 Term 2
Objectives and Outcomes
Due: Wednesday, 9th July, 12:00 (AEST)
Submission is through inspera. Prose should be typed, not handwritten.
Discussion of assignment material with others is permitted, but the work submitted must be your own inline with the University’s plagiarism policy.
Problem 1 (20 marks)
Let R ⊆ S × S be any binary relation on a set S. Consider the sequence of relations R0, R1, R2, . . ., defined as follows:
R0 := I = {(x, x) : x ∈ S}, and
Rn+1 := Rn ∪ (R; Rn ) for n ≥ 0
(a) Prove that for all i, j ∈ N, if i ≤ jthen Ri ⊆ Rj. Hint: Let Pi(j) be the proposition that Ri ⊆ Rj and prove that Pi(j) holds for all j ≥ i.
(b) Let P(n) be the proposition that for all m ∈ N: Rn; Rm = Rn+m . Prove that P(n) holds for all n ∈ N. Hint: Use results from Assignment 1
(c) Prove that if there exists i ∈ N such that Ri = Ri+1, then Rj = Ri for all j ≥ i.
(d) If |S| = k, explain why Rk2 = Rk2 +1 .
(e) If |S| = k, show that Rk2 is transitive.
(f) If |S| = k show that Rk2 is the minimum (with respect to ⊆) of all reflexive and transitive relations that contain R.
Remark
The relation at the limit a as n tends to infinity, R∗ = limn→ ∞Ri, is known as the reflexive, transitive closure of R, and is closely connected to the Kleene star operator.
Problem 2 (20 marks)
A binary tree is a data structure where each node is linked to at most two successor nodes:
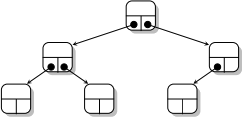
If we include empty binary trees (trees with no nodes) as part of the definition, then we can simplify the description of the data structure. Rather than saying a node has 0, 1, or 2 successor nodes, we can instead say that a node has exactly two children, where a child is a binary tree. That is, we can abstractly define the structure of a binary tree as follows:
• (B): An empty tree, τ
• (R): An ordered pair (Tleft, Tright) where Tleft and Tright are trees.
So, for example,the above tree would be defined as the tree T where:
T = (T1, T2), where
T1 = (T3, T4) and T2 = (T5, τ), where
T3 = T4 = T5 = (τ, τ)
That is,
T = ( ((τ, τ), (τ, τ)), ((τ, τ), τ))
A leaf in a binary tree is a node that has no successors (i.e. it is of the form (τ, τ)). Afully-internal node in a binary tree is a node that has exactly two successors (i.e. it is of the form (T1, T2) where T1, T2 ![]() τ). The example above has 3 leaves (T3, T4, and T5) and 2 fully-internal nodes (T and T1). For technical reasons (that will become apparent) we assume that an empty tree has 0 leaves and 一1 fully-internal nodes.
τ). The example above has 3 leaves (T3, T4, and T5) and 2 fully-internal nodes (T and T1). For technical reasons (that will become apparent) we assume that an empty tree has 0 leaves and 一1 fully-internal nodes.
(a) Based on the recursive definition above, recursively define a function count(T) that counts the number of nodes in a binary tree T.
(b) Based on the recursive definition above, recursively define a function leaves(T) that counts the number of leaves in a binary tree T
(c) Based on the recursive definition above, recursively define a function internal(T) that counts the num- ber of fully-internal nodes in a binary tree T.
(d) If T is a binary tree, let P(T) be the proposition that leaves(T) = internal(T) + 1. Prove that P(T) holds for all binary trees T. Your proof should be based on your answers given in (b) and (c).
Problem 3 (12 marks)
Consider the following two algorithms that naïvely compute the sum and product of two n x n matrices.
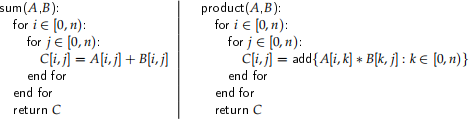
Assuming that adding and multiplying matrix elements can be carried out in O(1) time, and add will add the elements of a set S in O(|S|) time:
(a) Give an asymptotic upper bound, in terms of n, for the running time of sum. (3 marks)
(b) Give an asymptotic upper bound, in terms of n, for the running time of product. (3 marks)
When n is even, we can define a recursive procedure for multiplying two n × n matrices as follows. First, break the matrices into smaller submatrices:
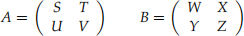
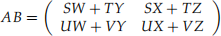
where SW + TY, SX + TZ, etc. are sums of products of the smaller matrices. If n is a power of 2, each smaller product (SW, TY, etc) can be computed recursively, until the product of 1 × 1 matrices needs to be computed – which is nothing more than a simple multiplication, taking O(1) time.
Assume n is a power of 2, and let T(n) be the worst-case running time for computing the product of two n × n matrices using this method.
(c) With justification, give a recurrence equation for T(n). (4 marks)
(d) Find an asymptotic upper bound for T(n). (2 marks)
Problem 4 (18 marks)
Recall from Assignment 1 the neighbourhood of eight houses:

As before, each house wants to set up its own wi-fi network, but the wireless networks of neighbouring houses – that is, houses that are either next to each other (ignoring trees) or over the road from one another (directly opposite) – can interfere, and must therefore be on different channels. Houses that are sufficiently far away may use the same wi-fi channel. Again we would like to solve the problem of finding the minimum number of channels needed, but this time we will solve it using techniques from logic and from probability. Rather than directly asking for the minimum number of channels required, we ask if it is possible to solve it with just 2 channels. So suppose each wi-fi network can either be on channel hi or on channel lo. Is it possible to assign channels to networks so that there is no interference?
(a) Formulate this problem as a problem in propositional logic. Specifically:
(i) Define your propositional variables (4marks)
(ii) Define any propositional formulas that are appropriate and indicate what propositions they represent. (4 marks)
(iii) Indicate how you would solve the problem (or show that it cannot be done) using propositional logic. It is sufficient to explain the method, you do not need to provide a solution. (2 marks)
(iv)* Explain how to modify your answer(s) to (i) and (ii) if the goal was to see if it is possible to solve with 3 channels rather than 2. (4 marks)
(b) Suppose each house chooses, uniformly at random, one of the two network channels. What is the probability that there will be no interference? (4 marks)
Problem 5 (16 marks)
Recall from Problem 2 the definition of a binary tree data structure: either an empty tree, or a node with two children that are trees.
Let T(n) denote the number of binary trees with n nodes. For example T(3) = 5 because there are five binary trees with three nodes:
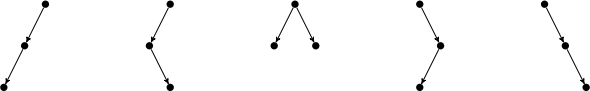
(a) Using the recursive definition of a binary tree structure, or otherwise, derive a recurrence equation for T(n). (6 marks)
A full binary tree is a non-empty binary tree where every node has either two non-empty children (i.e. is a fully-internal node) or two empty children (i.e. is a leaf).
(b) Using observations from Assignment 2, or otherwise, explain why a full binary tree must have an odd number of nodes. (2 marks)
(c) Let B(n) denote the number of full binary trees with n nodes. Derive an expression for B(n), involving T(n′) where n′ ≤ n. Hint: Relate the internal nodes of a full binary tree to T(n). (4 marks)
A well-formed formula is in Negated normal form if it consists of just ∧, ∨, and literals (i.e. propositional variables or negations of propositional variables). For example, (p ∨ (¬q ∧ ¬r)) is in negated normal form; but (p ∨ ¬(q ∨ r)) is not.
Let F(n) denote the number of well-formed, negated normal form formulas1 there are that use precisely n propositional variables exactly one time each. So F(1) = 2, F(2) = 16, and F(4) = 15360.
(d) Using your answer for part (c), give an expression for F(n). (4 marks)
Remark
The T(n) are known as the Catalan numbers. As this question demonstrates they are very useful for counting various tree-like structures.
Problem 6
Consider the following directed graph: (12 marks)
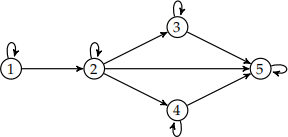
![]()
and consider the following process:
• Initially, start at 1.
• At each time step, choose one of the outgoing edges from your current location uniformly at random, and follow it to the next location. For example, if your current location was 2, then with probability ![]()
![]()
![]()
![]()
Let p1(n), p2(n), p3(n), p4(n), p5(n) be the probability your location after n time steps is 1, 2, 3, 4, or 5 respectively. So p1(0) = 1 and p2(0) = p3(0) = p4(0) = p5(0) = 0.
(a) Express p1(n + 1), p2(n + 1), p3(n + 1), p4(n + 1), and p5(n + 1) in terms of p1(n), p2(n), p3(n), p4(n), and p5(n). (5 marks)
(b) Prove ONE of the following:
(i) For all n ∈ N: p1(n ![]() (4 marks)
(4 marks)
(ii) For all n ∈ N: p2(n) = 2 ![]()
![]() (5 marks)
(5 marks)
(iii) For all n ∈ N: p3(n) = p4(n) = (n ![]()
![]() (6 marks)
(6 marks)
![]() (iv) For all n ∈ N: p5(n) = 1 − (2n − 1) (7 marks)
(iv) For all n ∈ N: p5(n) = 1 − (2n − 1) (7 marks)
Note
Clearly state which identity you are proving. A maximum of 7 marks is available for this question and marks will be awarded based on level of technical ability demonstrated. You may assume the identities which you are not proving.
Remark
This is an example of a Markov chain– a very useful model for stochastic processes.
Advice on how to do the assignment
Collaboration is encouraged, but all submitted work must be done individually without consulting some- one else’s solutions in accordance with the University’s “Academic Dishonesty and Plagiarism” policies.
• Assignments are to be submitted via inspera.
• When giving answers to questions, we always would like you to prove/explain/motivate your an- swers. You are being assessed on your understanding and ability.
• Be careful with giving multiple or alternative answers. If you give multiple answers, then we will give you marks only for your worst answer, as this indicateshow well you understood the question.
• Some of the questions are very easy (with the help of external resources). You may make use of external material provided it is properly referenced2– however, answers that depend too heavily on external resources may not receive full marks if you have not adequately demonstrated ability/un-
derstanding.
• Questions have been given an indicative difficulty level:
This should betaken as a guide only. Partial marks are available in all questions, and achievable by students of all abilities.
2023-08-08