COMP2123 Tutorial 8: Graphs algorithms s1 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP2123
Tutorial 8: Graphs algorithms
s1 2023
|
Warm-up |
Problem 1. Consider Dijkstra’s shortest path algorithm for undirected graphs. What changes (if any) do we need to make to this algorithm for it to work for directed graphs and maintain its running time?
Problem 2. Consider the following weighted undirected graph G:
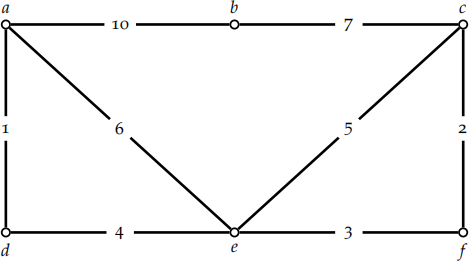
Your task is to compute a minimum weight spanning tree T of G:
a) Which edges are part of the MST?
b) In which order does Kruskal’s algorithm add these edges to the solution.
c) In which order does Prim’s algorithm (starting from a) add these edges to the solution.
|
Problem solving |
Problem 3. Let G = (V, E) be an undirected graph with edge weights w : E → R+ . For all e ∈ E, define w1 (e) = αw(e) for some α > 0, w2 (e) = w(e) + β for some β > 0, and w3 (e) = w(e)2 .
a) Suppose p is a shortest s-t path for the weights w. Is p still optimal under w1 ? What about under w2? What about under w3 ?
b) Suppose T is minimum weight spanning tree for the weights w. Is T still optimal under w1? What about under w2? What about under w3 ?
Problem 4. It is not uncommon for a given optimization problem to have multiple optimal solutions. For example, in an instance of the shortest s-t path problem, there could be multiple shortest paths connecting s and t. In such situations, it may be desirable to break ties in favor of a path that uses the fewest edges.
Show how to reduce this problem to a standard shortest path problem. You can assume that the edge lengths ℓ are positive integers.
a) Let us define a new edge function ℓ\(e) = Mℓ(e) for each edge e. Show that if P and Q are two s-t paths such that ℓ(P) < ℓ(Q) then ℓ\(Q) − ℓ\(P) ≥ M.
b) Let us define a new edge function ℓ\\(e) = Mℓ(e) + 1 for each edge e. Show that if P and Q are two s-t paths such that ℓ(P) = ℓ(Q) but P uses fewer edges than Q then ℓ\\(P) < ℓ\\(Q).
c) Show how to set M in the second function so that the shortest s-t path under ℓ\\ is also shortest under ℓ and uses the fewest edges among all such shortest paths.
Problem 5. Consider the following generalization of the shortest path problem where in addition to edge lengths, each vertex has a cost. The objective is to find an s-t path that minimizes the total length of the edges in the path plus the cost of the
vertices in the path. Design an efficient algorithm for this problem.
Problem 6. Consider the improving-mst algorithm for the MST problem.
|
1: function improving-mst(G, w) 2: T ← some spanning tree of G 3: for e ∈ E / T do 4: T ← T + e 5: C ← unique cycle in T 6: f ← heaviest edge in C 7: T ← T − f 8: return T |
Prove its correctness and analyze its time complexity. To simplify things, you can assume the edge weights are distinct.
Problem 7. Consider the reverse-mst algorithm for the MST problem.
|
1: function reverse-mst(G, w) 2: Sort edges in decreasing weight w 3: T ← E 4: for e ∈ E in decreasing weight do 5: if T − e is connected then 6: T ← T − e 7: return T |
Prove its correctness and analyze its time complexity. To simplify things, you can assume the edge weights are distinct.
Problem 8. A computer network can be modeled as an undirected graph G = (V, E) where vertices represent computers and edges represent physical links between computers. The maximum transmission rate or bandwidth varies from link to link; let b(e) be the bandwidth of edge e ∈ E. The bandwidth of a path P is defined as
the minimum bandwidth of edges in the path, i.e., b(P) = mine∈P b(e).
Suppose we number the vertices in V = {v1, v2, . . . , vn}. Let B ∈ Rn×n be a matrix where Bij is the maximum bandwidth between vi and vj . Give an algorithm for computing B. Your algorithm should run in O(n3 ) time.
2023-06-24