Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

COMP2123

Tutorial 7: Graphs

s1 2023

Problem 1. Consider the following undirected graph.

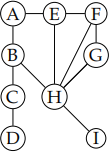
a) Starting from A, give the layers the breadth-first search algorithm finds.

b) Starting from A, give the order in which the depth-first search algorithm visits the vertices.

Problem 2. An undirected graph G = (V, E) is said to be bipartite if its vertex set V can be partitioned into two sets A and B such that E ⊆ A × B. Design an O(n + m) algorithm to test if a given input graph is bipartite using the following guide:

a) Suppose we run BFS from some vertex s ∈ V and obtain layers L1, . . . , Lk . Let (u, v) be some edge in E. Show that if u ∈ Li and v ∈ Lj then |i − j| ≤ 1.

b) Suppose we run BFS on G. Show that if there is an edge (u, v) such that u and v belong to the same layer then the graph is not bipartite.

c) Suppose G is connected and we run BFS. Show that if there are no intra-layer edges then the graph is bipartite.

d) Put together all the above to design an O(n + m) time algorithm for testing bipartiness.

Problem 3.   Give an O(n) time algorithm to detect whether a given undirected graph contains a cycle. If the answer is yes, the algorithm should produce a cycle. (Assume adjacency list representation.)

Problem 4. Let G = (V, E) be an n vertex graph. Let s and t be two vertices. Argue that if dist(s, t) > n/2 then there there exists a vertex u  s, t such that every path from s to t goes through u.

Problem 5.  In a directed graph, a get-stuck vertex has in-degree n − 1 and out- degree 0.  Assume the adjacency matrix representation is used.  Design an O(n) time algorithm to test if a given graph has a get-stuck vertex. Yes, this problem can be solved without looking at the entire input matrix.

Problem 6.  Let G be an undirected graph with vertices numbered 1 . . . n.  For a vertex i define small(i) = min{j : j is reachable from i}, that is, the smallest vertex reachable from i.  Design an O(n + m) time algorithm that computes small(i) for every vertex in the graph.

Problem 7. In a connected undirected graph G = (V, E), a vertex u ∈ V is said to be a cut vertex if its removal disconnects G; namely, G[V − u] is not connected.

The aim of this problem is to adapt the algorithm for cut edges from the lecture, to handle cut vertices.

a) Derive a criterion for identifying cut vertices that is based on the down-and-up[ ·] values defined in the lecture.

b) Use this criterion to develop an O(n + m) time algorithm for identifying all cut vertices.

Problem 8. Let T be a rooted tree. For each vertex u ∈ T we use Tu  to denote the subtree of T made up by u and all its descendants. Assume each vertex u ∈ T has a value A[u] associated with it. Let B[u] = min{A[v] : v ∈ Tu}. Design an O(n) time algorithm that given A, computes B.

Problem 9. Let G be a connected undirected graph. Design a linear time algorithm for finding all cut edges by using the following guide:

a) Derive a criterion for identifying cut edges that is based on the down-and-up[ ·] values defined in the lecture.

b) Use this criterion to develop an O(n + m) time algorithm for identifying all cut edges.