Physics 2301 Spring 2023 — Rotation Unit PRACTICE MIDTERM
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Physics 2301 Spring 2023 — Rotation Unit PRACTICE MIDTERM
The real will take place on Friday, March 3 at 10:20/11:30 am.
Rules ofthe Exam
This exam is designed to 55 minutes to complete.
The exam is open book, open notes, and is open to all material provided on the Physics 2301 course site in Carmen. Cal- culators and iPads (or similar devices, to access to course material on Carmen, TopHat, or Gradescope, or the electronic textbook) are allowed throughout the exam. Until the exam solutions are posted, do not discuss the contents ofthis exam with others— including other students—and do not use your electronic devices to look for help on the wider inter- net before you submit your work.
The exam consists of 100 points total, spread across 8 problems and 5 pages. The problems near the end account for more ofthe total points than the problems at the beginning, so be sure to budget time to complete the later problems.
For the problems that specify you must show all work for full credit, you should show your reasoning, the equations you’ve used, and all steps you’ve taken to arrive at your results. If you run out of space, you may use the back of any
page or scratch paper. Leave a note indicating where you are continuing your work.
Good luck, and have fun!

Problem 1 (10 points)
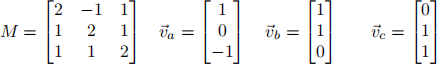
Which ofthe following statements are true? (circle each true statement)
(a) M is a diagonal matrix
(b) M is a symmetric matrix (Mij = Mji)
(c) v一a is an eigenvector of M with eigenvalue 1
(d) v一b is an eigenvector of M
(e) v一c is an eigenvector of M
(f) The eigenvalues of M are 2, 2, and 2.
Problem 2 (10 points)
A sphere of radius R rolls without slipping with given velocity v一 and
unspecified rotation vector ω一. In the drawing, point A at the bo计om
is momentarily at rest while the center B moves away into the page at
v一B = vyˆ. The point C (on the edge at displacement −R![]() from B) is mov-
from B) is mov-
ing out ofthe page at v一C = −vyˆ .
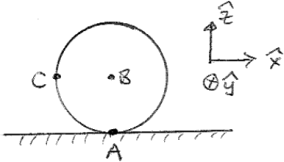
Which ofthe following statements are true? (Circle each true statement)
(a) The rotation vector is ω一 = ![]()
![]()
(b) The rotation vector is ω一 = ![]() ( −
( −![]() +2zˆ).
+2zˆ).
(c) The rotation vector is ω一 = ![]()
![]() .
.
(d) There is one more point (other than A) on the circle in the drawing that is at rest.
(e) At the moment shown, point A is the only point on the sphere at rest.
Problem 3 (10 points)
A stick of length 2R and mass m is fused at it midpoint to a point on hoop, con-
veniently enough also of mass m and radius R. The stick is tangent to the hoop,
and the center of mass ofthe system is (by symmetry) a distance R/2 above the
midpoint ofthe stick.

Which ofthe following are true about the principal moments and axes ofthe
inertia matrix around the combined object’s center of mass? (Circle all correct
answers)
(a) One principal moment of inertia is mR2
(b) One principal moment of inertia is ![]() mR2
mR2
(c) One principal moment of inertia is ![]() mR2
mR2
 moment of inertia is 1 mR2
moment of inertia is 1 mR2
(f) One principal moment of inertia is 0
(g) The x axis is a principal axis
(h) The y axis is a principal axis
(i) The z axis is a principal axis
Problem 4 (10 points)
IfA一 = Rrˆ +2Lzˆand ![]() = 3n
= 3n![]() +4nzˆ, then A一 ×
+4nzˆ, then A一 × ![]() is (mark the one correct answer)
is (mark the one correct answer)
(a) 14n2 rˆ +6nL![]()
(b) 6nLrˆ +4nR![]()
(c) −6nLrˆ − 4nR![]()
(d) −6nLrˆ − 4nR![]() +3nRXˆ
+3nRXˆ
Problem 5 (12 points)

A uniform disk of mass m and radius R floats in outer space and spins about its symmetry axis at angular speed ω0 . Along the symmetry axis, there is a massless stick, which happens to be length Ras well (see diagram). A point mass also of mass m with velocity v0 perpendicular to the symmetry axis hits the end ofthe stick and embeds itself, forming one rigid body of mass 2m. The incoming speed is v0 = ω0 R.
(a) What is the center of mass ofthe new system? (By symmetry, it should be somewhere along the stick).
(b) What are the principal axes and moments of inertia ofthe combined system (once stuck)?
(c) Write down the angular momentum vectorjust aier the collision, and find its components along each ofthe princi- pal axes from part b.
(d) How would you find how long it takes until the stick again points in the original direction? (You do not need to solve for this,just describe your strategy).
Problem 6 (24 points)
Show all work for full credit.
A stick of mass m and length l spins with frequency ω around an axis, as shown. The
stick makes an angle θ with the axis and is kept in its motion by two strings that are
perpendicular to the axis. What is the tension in the strings? (Ignore gravity.)
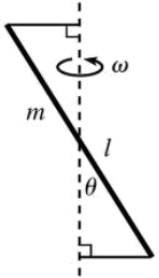
(a) Calculate the principal axes and moments of inertia ofthe stick, using the point on
the stick that is stationary as the coordinate origin.
(b) Find the angular momentum ofthe stick with respect to the coordinate origin from part a.
(c) Find the time derivative ofthe angular momentum.
(d) Find the net torque with respect to the coordinate origin from part a, in terms ofthe tension forces in the strings.
(e) Argue the tension forces should have identical magnitude, and find this magnitude.
Problem 7 (24 points)
Show all work for full credit.
A rotating system consists oftwo rigid bodies: a uniform, massless stick with one end a计ached to a pivot on the ground at A and the other end connected to a second pivot at the center (B) of a uniform disk. The disk has radius R and mass m. The disk rolls without slipping in a circle around point A, with its symmetry axis always parallel to the ground in the Tˆ direction of a cylindrical coordinate system. There is gravity g in the −zˆdirection, and we know the angle φ, and the frequency Ω for the wheel to circle around point A.
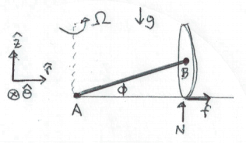
(a) If we were to consider the stick as a individual object rotating around the dashed vertical line in the diagram, its rota- tion vector would be −Ωzˆ. If we consider the disk separately as well, write down an expression for the rotation vector of the disk (at the instant pictured) in terms ofthe disk’s rotation frequency ω \ .
(b) Since the disk is rolling without slipping, so that the contact point between the disk and the ground traces a circle around point A, how are ω \ and Ω related? (Write down an equation involving the radius ofthe disk, R, and the angle φ .
(c) Write the torque equation for the disk using its center of mass (B) as the origin, and determine the friction force f from the ground.
(d) Write the torque equation for the combined stick and disk system, using the pivot A as the origin, and determine the normal force N between the disk and the ground.
2023-03-03