ST104 - 2021 - Statistical Laboratory

Practical 6: Assessed coursework 2

Important information

This practical session is assessed. The deadline for submission is 12 noon on Thursday, 13th May.

        Your reports should be submitted electronically on Moodle. Here is the link for submission: https://moodle.warwick.ac.uk/mod/assign/view.php?id=1043645. Also, make sure that you properly sub-mit your final version, and not only a draft submission. If you have any doubt or problems, let me know as soon as possible, so we can sort that out in time. Finally, the support office is really strict on submis-sion times, so try and submit at least a couple of hours before the deadline, and not literally last minute, so to prevent avoidable penalties.

        Please note that your report must be submitted in PDF. You should try and limit yourself to about 5 or 6 sides of A4, but without counting for any figures which may be needed. In particular, do not print very long vectors, if they are not required. You will notice that a few questions (or part of questions) need to be asnwered analytically. You may want to answer them by hand. That is fine, you can scan your handwritten work and include it as image in your report for example. Just try to make sure the report is still well structured.

        Also, please make sure you include your student ID code and lab group number and/or tutor name on the front sheet, but NOT your name!

        There will be a total of 40 marks for this assignment. The first exercise will carry 24 marks, and the second exercise will carry 12 marks. An additional 4 marks are allocated to the writing layout and general presentation of your report. So make sure to be clear when answering, give the requested answers, explain by using sentences to link your reasoning...

Exercises

1. Poisson process

In this exercise we study random arrivals on a time line, illustrating the duality between arrivals and waiting times, whcih shows an interesting connection between the Poisson distribution and the exponen-tial distribution. This example is inspired by real world phenomena. The arrivals can be something like customers entering a store, phone calls coming into a phone exchange, radioactive particles arriving at a counter, earthquakes occurring in a certain region, or typos you make in your R code for this exercise sheet.

Typical simplifying assumptions are:

● there are no exactly identical arrival times (so there’s never two events that happen simultaneously),

● their intensity is homogeneous over time (you don’t have “slow” periods and “fast” periods),

● their numbers in disjoint time intervals are independent (knowing how many events have happened already tells you nothing about how many will happen in future, as long as you know the intensity).

This leads to a model called Poisson arrival process with intensity λ (for some positive constant λ):

(i) The number N(I) of points in an interval I is a Poisson random variable with mean λ × length(I).

(ii) For disjoint intervals I1, . . . , Ij , the numbers of arrivals N(I1), . . . , N(Ij ) are mutually independent.

An equivalent description of this process involves the exponential distribution. It is obtained by shifting the perspective from arrivals to waiting times. Instead of counting arrivals in a given interval, we now measure inter-event times, that is, the time between consecutive arrivals:

The distribution of waiting time W1 until the first arrival is exponential (λ). W1 and the subsequent wait-ing times W2, W3, . . . between each arrival and the next are independent, all with the same exponential distribution.

1. Write a function countevents() that, given a vector V of length n, composed of n − 1 inter-event times and a specific time t (written at the end of the vector V ); counts the number of events that occur before t. So for example, applying countevents() to the vector (1, 4, 2, 5, 10) should return an output of 3, since the first three events take place within 10 time units, and the fourth event takes place after 10 time units. You may find the functions sum(), cumsum() and max() useful. (However, there is more than one way of doing it, so if you have found another methods that is perfectly fine.) Note that you need to pay attention to some particular cases: the total of the inter-event times may be shorter than the interval, or the first event may not have occurred before t: Test your function on a few numerical examples, including these in your report.

[4 marks]

2. Use the rexp function to generate several samples of m realisations from Exp(0.1), Exp(0.5) and Exp(1). Choose an appropriate number of samples and value of m for acceptable accuracy. Using these samples, estimate the first percentile for each of those three exponential distributions. That is, estimate the positive constant below which only 1% of all sample values occur, for each of the three distributions. You need include only those three estimates in your report, not the samples themselves.

[2 marks]

3. Now simulate a Poisson arrival process by using the waiting time description given above. This involves simulating inter-event times using rexp() and using countevents() to determine the number of counts.

Write a function poissonsimulation() that calculates the number of arrivals until time t in n such trials. The arguments should be the exponential parameter λ, the time t, and the number of counts n to be sampled. It should return a vector with n elements, corresponding to the counts. For this section, you may assume 0.1 ≤ λ ≤ 1, and 0 < t ≤ 1, otherwise the number of inter-event times you need to calculate will get too high. Even with this limitation though you will have to think carefully about how many inter-event times you need to calculate - briefly explain in your report the conclusion you came to regarding this. [If you do not see how many inter-event times to calculate, use 100. It will not give you the mark associated to that point, but it will allow you to continue even if you are stuck on that issue.]

Once complete your function should return a vector with n elements, each of which is a count. Using the function apply(), this function can be written up very brieflfly. However, it’s easy to make mistakes, so read the help files about this function very carefully. Otherwise, any other way, for example a for loop, would totally be acceptable if the function works. If you have done this correctly the values in the output vector should be samples from a Poisson distribution with parameter λt. Check this by generating 50 000 values where λ = t = 1 and finding the proportion of each value in the sample (you only need to consider the values you’ve actually generated). Then calculate the probability of each of these values for the Pois(1) distribution, and compare this to the proportions you found in your sample.

[7 marks]

4. Use the barplot() function (you will also need the table() function applied to the result vector to get the data into the right shape) to generate bar plots for the counts using the following combinations of n, λ, and t.

[2 marks]

5. Modify your poissonsimulation function so that inter-event times are modelled using a normal distribution N(µ, σ2 ) instead of an exponential distribution (you may need to add in code that prevents an inter-event time from ever being negative). Give the code for this modified function in your report. Generate bar plots for the counts using the following combinations of n, µ, σ and t. Describe the difference in the barplot shape between the first two barplots and the third, and explain why this difference exists.

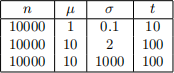
[9 marks]

2. Weibull distribution

Named after Swedish mathematician Waloddi Weibull (although it had already been identified and ap-plied before), the Weibull distribution has many applications, including (among others): survival analysis, extreme value theory, weather forecasting, finance/insurance, particle studies...

        The density function fX(x; k, λ) (or fX(x)) of a Weibull distribution W(k, λ) with shape parameter k > 0 and scale parameter λ > 0 is defined as:

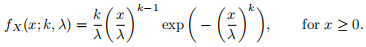
(a) Determine the cumulative distribution function FX(x), and then find the inverse function 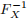of FX.

[3 marks]

(b) Describe an algorithm which uses the inverse transform method to generate n values sampled from a Weibull distribution.

[2 marks]

(c) Apply your methodology to generate a sample of 100000 values from Weibull(2,3). Plot a normalised histogram (like a probability density) of these realisations.

[2 marks]

(d) On that same histogram, by using (for example) the lines function, add a line that shows the probability density fuction of a Weibull(2,3) distribution.

[2 marks]

(e) By using only the U(0, 1) distribution as a source of randomness, find a way to calculate the following integral with R:

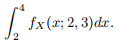
    [Hint: first, a suitable (linear) change of variable could be useful.]

    You can check your answer by hand or by using R functions.

[3 marks]